Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c) \(4sin3x\cdot sin2x\cdot cosx=2(cosx-cos5x)\cdot cosx\)
\(=2cos^2x-2cos5x\cdot cosx\)
\(=2cos^2x-cos4x-cos6x\)
\(=1+cos2x-cos4x-cos6x\)
d) \(4sin\dfrac{13x}{2}\cdot cosx\cdot cos\dfrac{x}{2}=4sin\dfrac{x}{2}\cdot cos\dfrac{x}{2}\cdot cosx\)
\(=2sinx\cdot cosx\)
\(=sin2x\)

\(A=2sin\dfrac{a+b}{2}cos\dfrac{a-b}{2}+2sin\dfrac{a+b}{2}cos\dfrac{a+b}{2}\)
\(=2sin\dfrac{a+b}{2}\left(cos\dfrac{a+b}{2}+cos\dfrac{a-b}{2}\right)\)
\(=2sin\dfrac{a+b}{2}.2cos\dfrac{a}{2}cos\dfrac{b}{2}\)
\(=4sin\dfrac{a+b}{2}cos\dfrac{a}{2}cos\dfrac{b}{2}\)

Chọn A.
Áp dụng công thức nhân đôi và chú ý: ![]() (đây là 2 góc phụ nhau)
(đây là 2 góc phụ nhau)
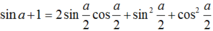
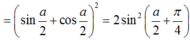
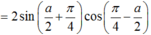
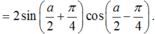

Lời giải:
$A=\sin ^2a-\sin ^2b=(\sin a-\sin b)(\sin a+\sin b)$
$B$ không biến đổi được. Bạn coi lại đề.