
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(VT=\dfrac{cot^2x}{1+cot^2x}\cdot\dfrac{1+tan^2x}{tan^2x}\)
\(=\dfrac{cot^2x}{\dfrac{1}{sin^2x}}\cdot\dfrac{\dfrac{1}{cos^2x}}{tan^2x}\)
\(=\dfrac{cot^2x}{tan^2x}\cdot\dfrac{1}{cos^2x}:\dfrac{1}{sin^2x}\)
\(=\dfrac{cot^2x}{tan^2x}\cdot\dfrac{sin^2x}{cos^2x}\)
\(=cot^2x\)
\(VP=\dfrac{tan^2x+cot^2x}{1+tan^4x}=\dfrac{\dfrac{sin^2x}{cos^2x}+\dfrac{cos^2x}{sin^2x}}{1+\dfrac{sin^4x}{cos^4x}}\)
\(=\dfrac{sin^4x+cos^4x}{sin^2x\cdot cos^2x}:\dfrac{cos^4x+sin^4x}{cos^4x}\)
\(=\dfrac{sin^4x+cos^4x}{sin^2x\cdot cos^2x}\cdot\dfrac{cos^4x}{cos^4x+sin^4x}=\dfrac{cos^2x}{sin^2x}=cot^2x\)
=>VT=VP
b:
\(\dfrac{tan^2x-cos^2x}{sin^2x}+\dfrac{cot^2x-sin^2x}{cos^2x}\)
\(=\dfrac{\left(\dfrac{sinx}{cosx}\right)^2-cos^2x}{sin^2x}+\dfrac{\left(\dfrac{cosx}{sinx}\right)^2-sin^2x}{cos^2x}\)
\(=\dfrac{sin^2x-cos^4x}{cos^2x\cdot sin^2x}+\dfrac{cos^2x-sin^4x}{sin^2x\cdot cos^2x}\)
\(=\dfrac{sin^2x+cos^2x-cos^4x-sin^4x}{cos^2x\cdot sin^2x}\)
\(=\dfrac{1-\left(cos^2x+sin^2x\right)^2+2\cdot cos^2x\cdot sin^2x}{cos^2x\cdot sin^2x}\)
\(=\dfrac{2\cdot cos^2x\cdot sin^2x}{cos^2x\cdot sin^2x}=2\)

\(\dfrac{1+cos2x-sin2x}{cos2x}=\dfrac{1+2cos^2x-1-2sinx.cosx}{cos^2x-sin^2x}=\dfrac{2cosx\left(cosx-sinx\right)}{\left(cosx-sinx\right)\left(cosx+sinx\right)}\)
\(=\dfrac{2cosx}{cosx+sinx}=\dfrac{2}{\dfrac{cosx}{cosx}+\dfrac{sinx}{cosx}}=\dfrac{2}{1+tanx}\)

Chọn A.
Ta có C = (1-sin2x) cot2x + 1 - cot2x.
= (1 - sin2x - 1) cot2x + 1
= -sin2x.cot2x + 1 = -cos2x + 1 = sin2x.

Đáp án: C
Ta có:
A = (1 - sin 2 x ) c o t 2 x + (1 - c o t 2 x ) = c o t 2 x - sin 2 x . c o t 2 x + 1 - c o t 2 x
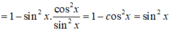

a) \(B=\dfrac{sin^4x-cos^4x+cos^2x}{2\left(1-cosx\right)\left(1+cosx\right)}\)
\(B=\dfrac{\left(sin^2x\right)^2-\left(cos^2x\right)^2+cos^2x}{2\left(1-cos^2x\right)}\)
\(B=\dfrac{\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)+cos^2x}{2\left(sin^2x+cos^2x-cos^2x\right)}\)
\(B=\dfrac{sin^2x-cos^2x+cos^2x}{2sin^2x}=\dfrac{sin^2x}{2sin^2x}=\dfrac{1}{2}\)
b) \(\dfrac{1+sin2x-cos2x}{1+sin2x+cos2x}=tanx\)
\(VT=\dfrac{1+2sinx.cosx-\left(1-2sin^2x\right)}{1+2sinx.cosx+2cos^2x-1}\)
\(VT=\dfrac{1+2sinx.cosx-1+2sin^2x}{2sinx.cosx+2cos^2x}\)
\(VT=\dfrac{2sinx.cosx+2sin^2x}{2sinx.cosx+2cos^2x}\)
\(VT=\dfrac{2sinx\left(cosx+sinx\right)}{2cosx\left(sinx+cosx\right)}=\dfrac{sinx}{cosx}=tanx=VP\) ( đpcm )
p/s : sửa \(cos1x\rightarrow cos2x\)


\(=\left(\dfrac{2sinx.cosx}{cos2x}-\dfrac{sinx}{cosx}\right)\left(2sinx.cosx-\dfrac{sinx}{cosx}\right)\)
\(=sinx\left(\dfrac{2cosx}{cos2x}-\dfrac{1}{cosx}\right).sinx\left(2cosx-\dfrac{1}{cosx}\right)\)
\(=sin^2x\left(\dfrac{2cos^2x-\left(2cos^2x-1\right)}{cosx.cos2x}\right)\left(\dfrac{2cos^2x-1}{cosx}\right)\)
\(=sin^2x\left(\dfrac{1}{cosx.cos2x}\right)\left(\dfrac{cos2x}{cosx}\right)=\dfrac{sin^2x}{cos^2x}=tan^2x\)
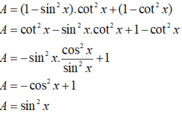
`B=(sin2x)/(tanx+cot2x)`
Tử ` = 2sinxcosx`
Mẫu `=(sinx)/(cosx) + (cos2x)/(sin2x)`
`=(sinx . sin2x + cosx .cos2x)/(2sinx cosx . cosx)`
`=(cos (2x-x))/(2sinxcos^2x)`
`=(cosx)/(2sinxcos^2x)`
`=1/(2sinxcosx)`
`=> B = sin^2 2x`
Lớp 8 nên không chắc ạ.
\(B=\dfrac{sin2x}{tanx+cot2x}=\dfrac{2sinx.cosx}{\dfrac{sinx}{cosx}+\dfrac{cos2x}{sin2x}}=\dfrac{2sinx.cosx}{\dfrac{sinx.sin2x+cos2x.cosx}{cosx.sin2x}}=\dfrac{2sinx.cosx}{\dfrac{.2sin^2x.cosx+cosx\left(2cos^2x-1\right)}{cosx.2sinx.cosx}}=\dfrac{2sinx.cosx.}{\dfrac{cosx\left(2sin^2x+2cos^2x-1\right)}{cos.2sinx.cosx}}=\dfrac{2sinx.cosx}{\dfrac{1}{2sinx.cosx}}=2sinx.cosx.2sinx.cosx=sin^22x.\)