

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Điều kiện: 1 ≤ x ≤ 3
bpt 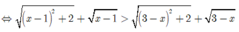
Xét
f ( t ) = t 2 + 2 + t , t ≥ 0 f ' ( t ) = t 2 t 2 + 2 + 1 2 t , ∀ t > 0
Do đó hàm số đồng biến trên [ 0 ; + ∞ ) .
Từ (1) suy ra f(x-1) >f(3-x) hay x-1> 3-x
Suy ra : x> 2
So với điều kiện, bpt có tập nghiệm là S= (2; 3]
Do đó; a=2; b=3 và b-a=1
Chọn A.

Điều kiện: 1≤ x≤ 3
Với điều kiện trên bpt
( x - 1 ) 2 + 2 + x - 1 > ( 3 - x ) 2 + 2 + 3 - x
Xét f ( t ) = t 2 + 2 + t v ớ i t ≥ 0
có f ' ( t ) = 1 2 t 2 + 2 + 1 2 t > 0 ∀ t > 0
Do đó hàm số đồng biến trên [0; +∞).
Khi đó (1) tương đương f(x-1) > f(3-x) hay x-1> 3-x
Suy ra x > 2
So với điều kiện, bpt có tập nghiệm là (2; 3] và 4a- b= 5
Chọn C.

Điều kiện: -2 ≤ x≤ 4.
Xét 2 x 3 + 3 x 2 + 6 x + 16 - 4 - x trên đoạn [ -2; 4].
Có
f ' ( x ) = 3 ( x 2 + x + 1 ) 2 x 3 + 3 x 2 + 6 x + 16 + 1 2 4 - x > 0 ∀ x ∈ ( - 2 ; 4 ) .
Do đó hàm số đồng biến trên [-2; 4]
Bất phương trình đã cho trở thành f(x)≥ f(1) =2 3
Kết hợp với điều kiện hàm số đồng biến suy ra x≥1.
So với điều kiện, tập nghiệm của bpt là [1; 4].
Do đó; a2+ b2= 17.
Chọn D.