Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đoán đề: \(\dfrac{x^2-1}{\left(x+1\right)\left(x^2-x-6\right)}\ge0\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x-3\right)\left(x+2\right)}\ge0\)
Xét x-1=0 <=> x=1
x+1=0 <=> x=-1
x-3=0 <=> x=3
x+2=0 <=>x=-2
Bảng xét dấu:
Để VT \(\ge0\) <=> x\(\in\left(-2;-1\right)\cup\left(3;+\infty\right)\cup\left\{1\right\}\)

ĐK: ` x \ne 0; x \ne1`
`(x-1)/x>=(3x-1)/(x-1)`
`<=>((x-1)^2-x(3x-1))/(x(x-1))>=0`
`<=> -((2x-1)(x+1))/(x(x-1)) >= 0`
`<=> ((2x-1)(x+1))/(x(x-1)) <= 0`
Bảng xét dấu bạn tự kẻ nkaaaaa.
Vậy `S=[-1;0) \cup [1/2 ;1)`.

Để pt có hai nghiệm <=> \(\Delta\ge0\)\(\Leftrightarrow16m^2-64m+48\ge0\)
\(\Leftrightarrow m\in R\backslash\left(1;3\right)\)
Có \(x_1+x_2-2x_1x_2< 8\)
\(\Leftrightarrow2\left(2m-3\right)-2\left(4m-3\right)< 8\)
\(\Leftrightarrow-4m-8< 0\)
\(\Leftrightarrow m>-2\)
Kết hợp với đk => \(m\in\left(-2;1\right)\cup\left(3;+\infty\right)\cup\left\{1;3\right\}\)

Ta có 2x – 4 >0
* Xét bất phương trình: mx – 1 <0 (*)
+ Nếu m = 0 thì ( *) luôn đúng với mọi x.
Khi đó, tập nghiệm của hệ bất phương trình là ( 2 ; + ∞ ) .
+ Nếu m > 0 thì từ (*) ⇔ m x < 1 ⇔ x < 1 m
Trong trường hợp này thì tập nghiệm của hệ bất phương trình không thể là ( 2 ; + ∞ ) .
+ Nếu m < 0 thì từ (*) ⇔ m x < 1 ⇔ x < 1 m
Do đó, để hệ bất phương trình đã cho có tập nghiệm là ( 2 ; + ∞ ) khi và chỉ khi 1 m < 2 ( luôn đúng vì m < 0).
Vậy tập hợp các giá trị m thỏa mãn là m ≤ 0 .

\(\Leftrightarrow\dfrac{mx^2-5x+m-4}{mx^2-4x+m-3}>0\)
BPT đã cho có tập nghiệm là R khi và chỉ khi:
\(\left\{{}\begin{matrix}\Delta_1=25-4m\left(m-4\right)< 0\\\Delta'_2=4-m\left(m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4m^2+16m+25< 0\\-m^2+3m+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< \dfrac{4-\sqrt{41}}{2}\\m>\dfrac{4+\sqrt{41}}{2}\end{matrix}\right.\)

Ta có: ( 1 ) ⇔ x ≤ - m . Tập nghiệm của (1) là ( - ∞ ; - m ] .
( 2 ) ⇔ x > 5 . Tập nghiệm của (2) là 5 ; + ∞ .
Hệ đã cho có nghiệm khi và chỉ khi ( - ∞ ; - m ] ∩ 5 ; + ∞ . Điều này xảy ra khi và chỉ khi 5 < - m ⇔ m < - 5 .
Đáp án là A.
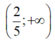
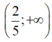
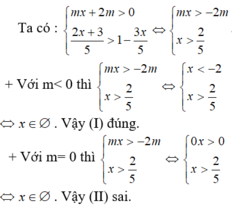
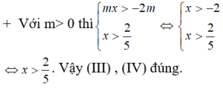
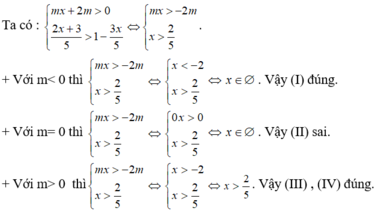
TH1: `m=0 `
`2x>0 <=> x>0`
`=>` Không thỏa mãn.
TH2: `m>0`
Bất PT có tập nghiệm là `RR <=> \Delta'<0`
`<=> (m-1)^2-m.4m<0`
`<=> m<-1 ; 1/3 <m`
Vậy `m in (0;+∞)` thỏa mãn.
TH1 là m=0 thì TH2 là \(m\ne0\)
Bpt có tập nghiệm là R <=> \(\left\{{}\begin{matrix}a>0\\\Delta'< 0\end{matrix}\right.\)
Đáp án: m\(\in\left(\dfrac{1}{3};+\infty\right)\)