Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\hept{\begin{cases}x+m\le0\\-x+5< 0\end{cases}\hept{\begin{cases}x\le-m\\x< -5\end{cases}\hept{\begin{cases}x\in\left(-\infty;-m\right)\\x\in\left(-\infty;-5\right)\end{cases}}}}\)bạn sửa lại chỗ trên nha là nửa khoảng
\(+-m\ge-5\)
\(m\le5< =>\)tập nghiệm của HPT \(S=\left(-m;-\infty\right)\)
\(+-m< 5\)
\(m>5< =>\)tập nghiệm của HPT \(S=\left\{-\infty;-5\right\}\)


a) \(2m^2-m-5>0\)(1)
\(\Delta=1+41=42\)Nghiệm của pt (1) là \(\Rightarrow m_1=\dfrac{1-\sqrt{42}}{4};m_2=\dfrac{1+\sqrt{42}}{4}\)
=> nghiệm BPT (1) là:
\(\left[{}\begin{matrix}m< \dfrac{1-\sqrt{42}}{4}\\m>\dfrac{1+\sqrt{42}}{4}\end{matrix}\right.\)
câu b
\(\Delta=1+4.9=37\)Nghiệm pt là \(m_1=\dfrac{1-\sqrt{37}}{2};m_2=\dfrac{1+\sqrt{37}}{2}\)
Nghiệm BPT là: \(\dfrac{1-\sqrt{37}}{2}< m< \dfrac{1+\sqrt{37}}{2}\)

Nhận xét rằng khi thay x=0 vào hệ bất phương trình, ta được :
\(\begin{cases}0-1<3-0\\m.0+1>0\end{cases}\) \(\Leftrightarrow\begin{cases}-1<3\\1>0\end{cases}\)
Hệ này luôn đúng với mọi \(m\in R\)
Vậy với mọi \(m\in R\) , hệ bất phương trình đã cho luôn có ít nhất một nghiệm (x=0).
Do đó với \(m\in R\) hệ bất phương trình đã cho luôn có nghiệm

a)
Để \(5x^2-x+m>0\) thì:
\(\Delta< 0\Rightarrow1-20m< 0\Rightarrow m>\dfrac{1}{20}\)
b)
\(mx^2-10x-5< 0\)
Xét \(m=0\) ta có: \(-10x-5< 0\)\(\Leftrightarrow x>\dfrac{1}{2}\) (loại)
Xét \(m\ne0\). Theo định lý về dấu tam thức bậc hai:
\(mx^2-10x-5< 0\)\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\25+5m< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m< -5\end{matrix}\right.\)\(\Leftrightarrow m< -5\).
Vậy với \(m< -5\) thì \(mx^2-10x-5< 0\).
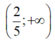
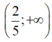
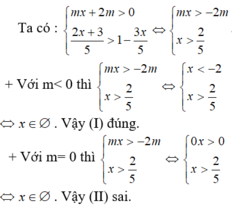
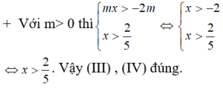
Chọn D