Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+ Bảng biến thiên:
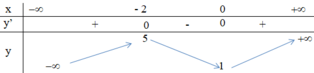
Kết luận:
Hàm số đồng biến trên các khoảng (-∞; -2) và (0; +∞).
Hàm số nghịch biến trên khoảng (-2; 0).
Hàm số đạt cực tiểu tại x = 0 ; y C T = 1 .
Hàm số đạt cực đại tại x = -2 ; y C Đ = 5 .
- Đồ thị:
+ Giao với Oy: (0; 1).
+ Đồ thị (C) đi qua điểm (–3; 1), (1; 5).
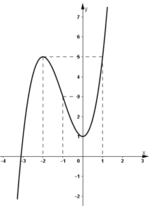
Đáp án B.
Tập xác định D = R.
y' = -3x2 + 6x – 3 = -3(x – 1)2 ≤ 0, ∀x ∈ R .Vậy hàm số luôn nghịch biến trên R
Chọn A
y ' = - 3 x 2 + 6 x - 3 = - 3 ( x 2 - 2 x + 1 ) = - 3 ( x - 1 ) 2 ≤ 0 ∀x ∈ R. Hàm số luôn nghịch biến.
Chọn A
Tập xác định: D = ℝ
Đạo hàm: y ' = 3 x 2 - 6 x - 9
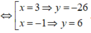
Bảng biến thiên
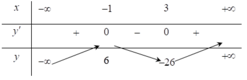
Hàm số đồng biến trên các khoảng - ∞ ; - 1 v à 3 ; + ∞
Do đó hàm số đồng biến trên khoảng 4 ; 5
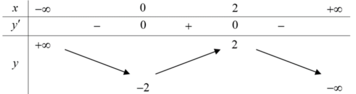
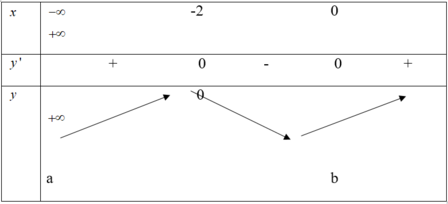
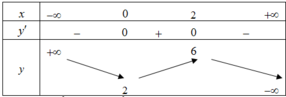
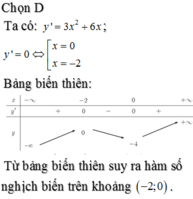
Đáp án B.
Ta có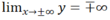
nên loại đáp án A.
Vì y(0) = -2 nên loại đáp án C.
Vì y’ = 0 có hai nghiệm 0; 2 nên chọn đáp án B