K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
31 tháng 8 2021
1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{ABC}=\widehat{ACB}\)
Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
Do đó: AH\(\perp\)BC
NT
àm ơn làm ơn hãy giúp mình câu này nha mình rất gấp rồi, mình thề sẽ quỳ gối trước bạn nào giúp mình
2
16 tháng 12 2021
a: Xét ΔABM và ΔCDM có
MA=MC
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔCDM
16 tháng 12 2021
a) Xét tam giác ABM và tam giác CDM có:
+ AM = CM (cho M là trung điểm của AC).
+ BM = DM (gt).
+ \(\widehat{AMB}=\widehat{CMD}\) (2 góc đối đỉnh).
\(\Rightarrow\) Tam giác ABM = Tam giác CDM (c - g - c).
b) Ta có: \(\widehat{BAM}=\widehat{DCM}\) (Tam giác ABM = Tam giác CDM).
Mà 2 góc này ở vị trí so le trong.
\(\Rightarrow\) AB // CD (dhnb).
c) Xét tam giác ABN và tam giác ECN có:
+ BN = CN (N là trung điểm của BC).
+ \(\widehat{ANN}=\widehat{ENC}\) 2 góc đối đỉnh).
+ \(\widehat{ABN}=\widehat{ECN}\) (do AB // CD).
\(\Rightarrow\) Tam giác ABN = Tam giác ECN (g - c - g).
\(\Rightarrow\) CE = AB (2 cạnh tương ứng).
Mà AB = CD (Tam giác ABM = Tam giác CDM).
\(\Rightarrow\) CE = CD (cùng = AB).
\(\Rightarrow\) C là trung điểm của DE (đpcm).
d) Xét tam giác BDE có:
+ M là trung điểm của BD (do MD = MB).
+ C là trung điểm của DE (cmt).
\(\Rightarrow\) MC là đường trung bình.
\(\Rightarrow\) MC // BE và MC = \(\dfrac{1}{2}\) BE (Tính chất đường trung bình trong tam giác).
Lại có: MC = \(\dfrac{1}{2}\) MF (do MC = MF).
\(\Rightarrow\) BE = MF.
Xét tứ giác BMEF có:
+ BE = MF (cmt).
+ BE // MF (MC // BE; C thuộc MF).
\(\Rightarrow\) Tứ giác BMEF là hình bình hành (dhnb).
\(\Rightarrow\) ME cắt BF tại trung điểm của mỗi đường (Tính chất hình bình hành).
Mà O là trung điểm của ME (gt).
\(\Rightarrow\) O là trung điểm của BF.
\(\Rightarrow\) 3 điểm B; O; F thẳng hàng (đpcm).
23 tháng 9 2021
\(B=2022^0+\left(-1\right)^{2021}+\left(-\dfrac{3}{2}\right)^2:\sqrt{\dfrac{9}{4}}-\left|-\dfrac{2}{3}\right|\)
\(=1-1+\dfrac{9}{4}:\dfrac{3}{2}-\dfrac{2}{3}\)
\(=\dfrac{9}{4}\cdot\dfrac{2}{3}-\dfrac{2}{3}\)
\(=\dfrac{3}{2}-\dfrac{2}{3}\)
\(=\dfrac{5}{6}\)
20 tháng 11 2021
cậu học nhanh thế
xin lỗi cậu nhé, tớ chưa với được đến đấy đâu
ND
0
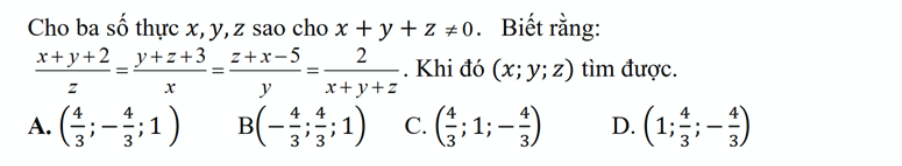
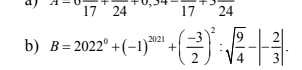
\(\dfrac{x+y+2}{z}=\dfrac{y+z+3}{x}=\dfrac{z+x-5}{y}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2=\dfrac{2}{x+y+z}\\ \Rightarrow\left\{{}\begin{matrix}x+y+2=2z\\y+z+3=2x\\z+x-5=2y\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y=2z-2\\y+z=2x-3\\z+x=2y+5\end{matrix}\right.\left(1\right)\)
Mà \(\dfrac{2}{x+y+z}=2\Rightarrow x+y+z=1\Rightarrow\left\{{}\begin{matrix}x+y=1-z\\y+z=1-x\\x+z=1-y\end{matrix}\right.\)
Thay vào hệ \(\left(1\right)\Rightarrow\left\{{}\begin{matrix}2z-2=1-z\\2x-3=1-x\\2y+5=1-y\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3z=3\\3x=4\\3y=-4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=-\dfrac{4}{3}\\z=1\end{matrix}\right.\Rightarrow\left(x;y;z\right)=\left(\dfrac{4}{3};-\dfrac{4}{3};1\right)\)
Chọn A