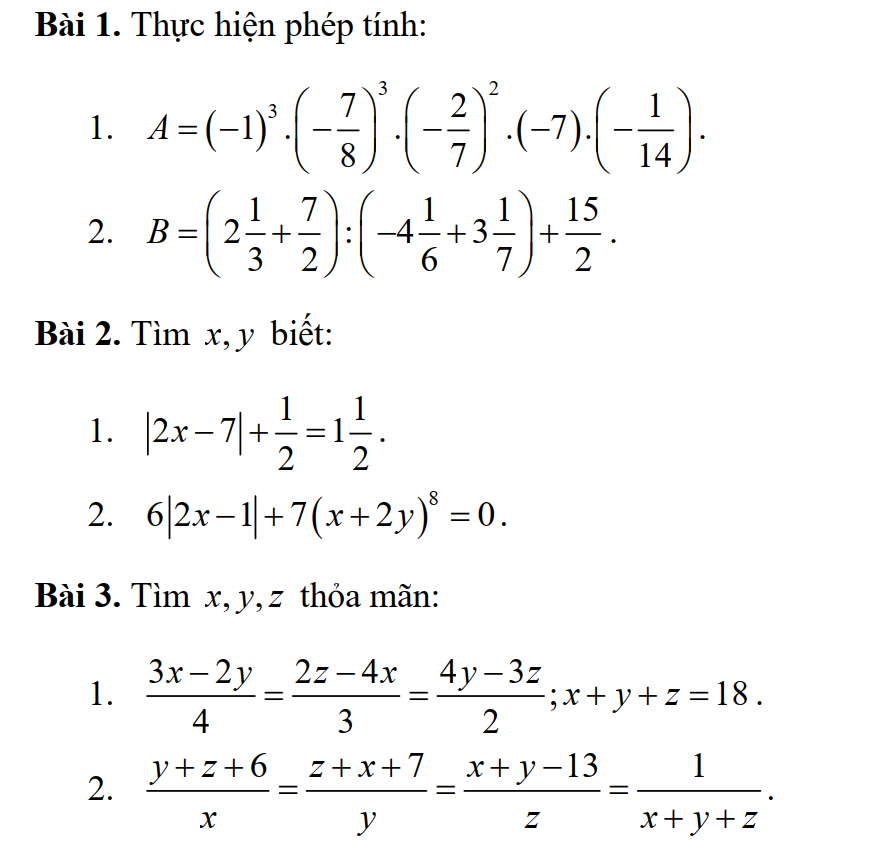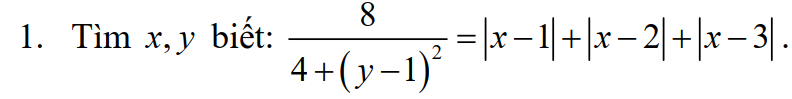K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VT
1
DM
17 tháng 11 2016
Có a . b = 54
-> (a;b) = (6;9), (9;6) , (54;1) , (1;54), (2;28), (28;2), (18;3) , (3;18) và các số âm của chúng
mà \(\frac{a}{2}=\frac{b}{3}\) => (a;b) = (9;6) , (54;1) , (1;54), (2;28), (28;2), (18;3) , (3;18) và các số âm của chúng không thỏa mãn yêu cầu đề bài.
-> (a;b) = (6;9) , (-6;-9)
Ta xét (a;b) = (6;9) -> \(\frac{a}{2}=\frac{b}{3}=\frac{6}{2}=\frac{9}{3}\) => a +b = 6 + 9 = 15
xét (a;b) = (-6;-9) -> \(\frac{a}{2}=\frac{b}{3}=-\frac{6}{2}=-\frac{9}{3}\) => a + b = -6 + (-9) = -15
Vậy GTNN của a + b là -15
17 tháng 11 2016
Xét 3 trường hợp:
- TH1: x < 12,2 ta có: (12,2 - x) + (22,6 - x) = 10
=> 34,8 - 2x = 10
=> 2x = 34,8 - 10 = 24,8
=> x = 24,8 : 2 = 12,4; không thỏa mãn x < 12,2
- TH2: \(12,2\le x< 22,6\) ta có: (x - 12,2) + (22,6 - x) = 10
=> 10,4 = 10; vô lý
- TH3: x \(\ge\) 22,6 ta có: (x - 12,2) + (x - 22,6) = 10
=> 2x - 34,8 = 10
=> 2x = 10 + 34,8 = 44,8
=> x = 44,8 : 2 = 22,4; không thỏa mãn x \(\ge\) 22,6
Vậy số giá trị của x thỏa mãn là 0
TK
23 tháng 11 2016
Nếu nhân tuổi của ba chị em với nhau được 36, điều đó có nghĩa là tuổi của họ sẽ rơi vào một trong 8 trường hợp sau đây:
36 = 2 x 3 x 6, tổng số tuổi của ba chị em là 11.
36 = 2 x 2 x 9, tổng số tuổi của ba chị em là 13.
36 = 4 x 9 x 1, tổng số tuổi của ba chị em là 14.
36 = 4 x 3 x 3, tổng số tuổi của ba chị em là 10.
36 = 18 x 2 x 1, tổng số tuổi của ba chị em là 21.
36 = 12 x 3 x 1, tổng số tuổi của ba chị em là 16.
36 = 6 x 6 x1, tổng số tuổi của ba chị em là 13.
36 = 36 x 1 x 1, tổng số tuổi của ba chị em là 38.
Dựa theo dữ kiện đầu bài đưa ra là "Cộng tuổi của ba chị em với nhau được 13", ta sẽ có hai trường hợp thỏa mãn là 2 + 2 +9 và 6 + 6 + 1.
Đây chính là lúc dữ kiện "Chị lớn nhất có tóc màu vàng hoe" được cho là vô dụng vào lúc đầu lại phát huy được tác dụng. Dữ kiện này cho thấy sẽ chỉ có một người chị lớn tuổi hơn cả. Ở hai trường hợp nêu trên, ta thấy trường hợp 2 + 2 + 9 là một chị và hai em sinh đôi, trong khi, trường hợp 6 + 6 +1 là hai chị sinh đôi và một em.
Chỉ có trường hợp một là thỏa mãn được yêu cầu của đầu bài. Như vậy, câu trả lời của bài toán này sẽ là một người chị lớn có 9 tuổi và hai em gái sinh đôi có cùng 2 tuổi.
KA
8 tháng 11 2021
- Viết hai số hữu tỉ dưới dạng hai phân số có cùng một mẫu dương (bằng cách quy đồng mẫu của chúng)
- Cộng, trừ hai tử số, mẫu chung giữ nguyên;
- Rút gọn kết quả (nếu có thể)
- HT
- Nhớ k nhen
26 tháng 8 2021
bài 2
1)
/2x-7/+\(\dfrac{1}{2}=1\dfrac{1}{2}\)
/2x-7/+\(\dfrac{1}{2}=\dfrac{3}{2}\)
/2x-7/=1
=> 2x-7=1 hoặc -2x+7 =1
2x=8 hoặc -2x=-6
x=4 hoặc x=3
26 tháng 8 2021
Bài 1:
1: Ta có: \(A=\left(-1\right)^3\cdot\left(-\dfrac{7}{8}\right)^3\cdot\left(-\dfrac{2}{7}\right)^2\cdot\left(-7\right)\cdot\left(-\dfrac{1}{14}\right)\)
\(=\dfrac{7^3}{8^3}\cdot\dfrac{4}{49}\cdot\dfrac{1}{2}\)
\(=\dfrac{343}{512}\cdot\dfrac{2}{49}\)
\(=\dfrac{7}{256}\)
AH
Akai Haruma
Giáo viên
26 tháng 8 2021
Lời giải:
$4+(y-1)^2\geq 4\Rightarrow \frac{8}{4+(y-1)^2}\leq 2$
Mặt khác, áp dụng BĐT $|a|+|b|\geq |a+b|$ ta có:
$|x-1|+|x-3|=|x-1|+|3-x|\geq |x-1+3-x|=2$
$\Rightarrow |x-1|+|x-2|+|x-3|\geq 2+|x-2|\geq 2$
Vậy $\frac{8}{4+(y-1)^2}\leq 2\leq |x-1|+|x-2|+|x-3|$
Dấu "=" xảy ra khi:
\(\left\{\begin{matrix} (y-1)^2=0\\ (x-1)(3-x)\geq 0\\ x-2=0\end{matrix}\right.\Leftrightarrow y=1; x=2\)