K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

AH
Akai Haruma
Giáo viên
19 tháng 8 2021
Lời giải:
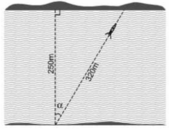
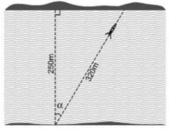
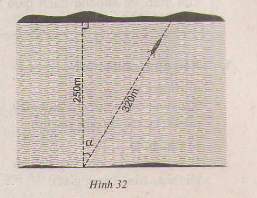
Giả sử dòng nước đẩy chiếc đò lệch đi một góc $\alpha$
Ta có: $\cos \alpha=\frac{250}{320}=\frac{25}{32}$
$\Rightarrow \alpha=38,62^0$

PN
4 tháng 10 2017
Chiếc đò lệch đi một góc bằng:
\(\cos\alpha=\frac{250}{320}\Rightarrow\alpha\approx38^o37'\)
4 tháng 10 2017
Chiếc đò lệch đi một góc bằng:
250/320=~38`37(sấp xỉ 38 độ 37)
ĐS:....(Tự điền nha)

CM
28 tháng 11 2019

Ta có khúc sông AC = 100m, quãng đường thuyền đi là BC = 180m
Góc lệch C ^
![]()
Vậy góc lệch là 56 0
Đáp án cần chọn là: A
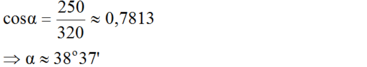
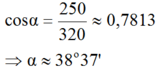

\(\Delta ABC\)vuông tại A có \(\widehat{B}=45^0\left(gt\right)\)\(\Rightarrow\Delta ABC\)vuông cân tại A \(\Rightarrow AB=AC\)
Mà \(AB=1039m\left(gt\right)\Rightarrow AC=1039m\)
Vì vận tốc đi bộ không đổi, thời gian đi quãng đường CD lại gấp đôi thời gian đi quãng đường AD nên \(CD=2AD\Rightarrow\frac{AD}{CD}=\frac{1}{2}\)(1)
Lại có \(\Delta ACD\) vuông tại A \(\Rightarrow\)\(\cos\widehat{D}=\frac{AD}{CD}\)(2)
Từ (1) và (2) \(\Rightarrow\cos\widehat{D}=\frac{1}{2}\Rightarrow\widehat{D}=60^0\)
\(\Delta ACD\)vuông tại A \(\Rightarrow\sin D=\frac{AC}{CD}\Rightarrow\sin60^0=\frac{1039}{CD}\Rightarrow CD=\frac{1039}{\sin60^0}=\frac{1039}{\frac{\sqrt{3}}{2}}\approx1200\left(m\right)\)
Vậy thực tế bạn An đã đi quãng đường CD dài khoảng 1200m