Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

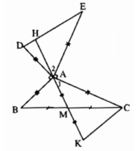
a) Xet tam giac ABM va tam giac CMK ta co:
AM=MK(gt)
BM=MC(M la trung diem BC)
goc AMB=goc KMC ( 2 goc doi dinh)
--> tam giac ABM= tam giac CMK (c-g-c)--> goc BAM = goc MKC hay goc BAM= goc AKC
ta co : goc AKC+goc ACK+goc KAC=180 ( tong 3 goc trong tam giac AKC)
ma goc AKC= goc BAM (cmt)
mem goc BAM+goc KAC+goc ACK=180
--> goc BAC+ goc ACK=180
---> 110+ goc ACK=180
---> goc ACK=180-110=70
b)ta co : goc BAC+goc BAD+ goc DAE+goc CAE=360
----> 110+90+ goc DAE+90=360
---> goc DAE=360-110-90-90=70
-ta co : AB=DA ( gt)
AB=CK ( tam giac ABM= tam giac MKC)
--> DA=CK
xet tam giac CAK va tam giacAED ta co"
CK=DA (cmt) , AC=AE (gt), goc ACK= goc DAE (=70)
--> tam giac CAK= tam giac AED ( c=g=c)
c) Keo dai KA cat DE tai H
ta co : goc HAE + goc EAC+goc CAK=180
ma goc AEH= goc CAK ( tam giac ADE= tam giac CAK)
nen goc HAE+goc AEH=180- goc EAC=180-90=90
ta co : goc HAE+goc AEH + goc AHE =180 ( tong 3 goc trong tam giac AHE)
--> 90+ goc AHE =180
--> goc AHE =180-90=90
--> AH vuong goc DE hay MA vuong goc DE

b/ ta có: Góc DAE = 360 - (90 . 2) - góc A = 180 - 110 = 70 độ
từ tam giác ABM = tam giác KCM => AB = CK
Xét tam giác CAK & tam giác AED có:
KCA = DAE (bằng 70 độ)
AD = CK (bằng AB)
AC = AE (gt)
=> tam giác CAK = tam giác AED (cgc)
b, vì tam giác ABM=tam giác KCM(câu a) =>AB=CK(2 cạnh tương ứng)
mà AB=AD(gt) =>KC=AD
Có DAE+DAB+EAC+BAC=3600=>DAE=3600-(DAB+EAC+BAC)
mả DAB=900(AD vuông góc vs AB-GT)
EAC=900(AE vuông góc vs AC-GT)
BAC=1100 (GT)
=>DAE=3600-(900+900+1100)=700
Có DAE=700(CMT)
ACK=700(câu a)
=>DAE=ACK(=700)
Xét tam giác CAK & tam giác AED có:
CK=AD(cmt)
CA=AE(gt)
DAE=ACK(cmt)
=>tam giác CAK=tam giác AED(c.g.c)
phần c mik k bit lm giúp nhé

a) \(\Delta\)ABM = \(\Delta\)KCM (c.g.c) => ^ABM = ^KCM (2 góc tương ứng) => AB // CK (2 góc so le trong bằng nhau)
=> ^BAC + ^ACK = 1800 (2 góc trong cùng phía) => ^ACK = 1800 - 1100 = 700
b) \(\Delta\)ABM = \(\Delta\)KCM (cmt) => AB = KC (2 cạnh tương ứng). Mà AB = AD => CK = AD
Ta có: ^BAC + ^BAD + ^CAE + ^DAE = 3600 => ^BAC + ^DAE = 1800
Mà ^BAC + ^ACK = 1800 => ^DAE = ^ACK hay ^DAE = ^KCA
Xét \(\Delta\)CAK và \(\Delta\)AED có: CK=AD; CA=AE; ^KCA = ^DAE => \(\Delta\)CAK = \(\Delta\)AED (đpcm).
c) Tia MA giao DE tại điểm H.
\(\Delta\)CAK = \(\Delta\)AED (cmt) => ^CAK = ^AED (2 góc tương ứng) hay ^CAK = ^AEH
Mà ^CAK + ^HAE = 1800 - ^CAE = 900 => ^AEH + ^HAE = 900 => \(\Delta\)AHE vuông tại H
=> AH vuông góc với DE hay MA vuông góc DE (đpcm).

Có: ∠DAE + ∠DAB + ∠BAC + ∠CAE = 360o
Mà ∠DAB = ∠CAE = 90o; ∠BAC = 110o
⇒ ∠DAE = 70o
⇒ ∠DAE = ∠ACK
+) Xét ΔCAK và ΔAED có:
AC = AE (gt)
∠ACK = ∠DAE (chứng minh trên)
CK = AD (cùng = AB)
⇒ ΔCAK = ΔAED (c.g.c)
