Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó:BCEF là tứ giác nội tiếp
b: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=180^0\)
Do đó: AEHF là tứ giác nội tiếp

góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc AFN=góc ACB
góc ACB=1/2*sđ cung AB=1/2(sđ cung AN+sđ cung NB)
góc AFN=1/2*sđ cung AN+1/2*sđ cung MB
=>sd cung AM=sđ cung AN
=>AM=AN

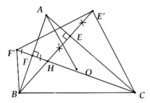
a, ∆CHE' cân tại C => C E ' H ^ = C H E ' ^
DBHF' cân tại B => B F ' H ^ = B H F ' ^
Mà => C H E ' ^ = B H F ' ^ (đối đỉnh)
=> C E ' H ^ = B F ' H ^
=> Tứ giác BCE'F' nội tiếp đường tròn tâm (O)
b, Có B F C ' ^ = B E ' C ^ = C H E ' ^ = C A B ^
Vậy A, F', E' cùng chắn BC dưới góc bằng nhau
=> 5 điểm B, F', A, E', C cùng thuộc một đường tròn tâm (O)
c, AF' = AE' (=AH) => AO là trung trực của EF => AO ^ E'F'. DHE'F' có EF là đường trung bình => EF//E'F'
=> AO ^ FE
d, A F H ^ = A E H ^ = 90 0 => AFHE nội tiếp đường tròn đường kính AH. Trong (O): Kẻ đường kính AD, lấy I trung điểm BC
=> OI = 1 2 AH, BC cố định => OI không đổi
=> Độ dài AH không đổi
=> Bán kính đường tròn ngoại tiếp ∆AEF không đổi

a: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>B,F,E,C cùng thuộc một đường tròn
b: Xét (O) có
ΔABA' là tam giác nội tiếp
AA' là đường kính
Do đó: ΔABA' vuông tại B
=>BA'\(\perp\)AB
mà CH\(\perp\)AB
nên BA'//CH
Xét (O) có
ΔACA' là tam giác nội tiếp
AA' là đường kính
Do đó: ΔACA' vuông tại C
=>AC vuông góc CA'
mà BH vuông góc AC
nên BH//A'C
Xét tứ giác BHCA' có
BH//CA'
BA'//CH
Do đó: BHCA' là hình bình hành

a: góc AEH=góc AFH=90 độ
=>AEHF nội tiếp đường tròn tâm I, I là trung điểm của AH
b: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp đường tròn đường kính BC
=>O là trung điểm của BC
c: góc IEO=góc IEH+góc OEH
=góc IHE+góc OBE
=góc OBE+góc OCE=90 độ
=>IE là tiếp tuyến của (O)
d: IE=IF
OE=OF
=>IO là trung trực của EF

a) Ta có: \(\widehat{CFB}=90^0\)(CF⊥AB)
nên F nằm trên đường tròn đường kính CB(Định lí)(1)
Ta có: \(\widehat{CEB}=90^0\)(BE⊥AC)
nên E nằm trên đường tròn đường kính CB(Định lí)(2)
Từ (1) và (2) suy ra F,E cùng nằm trên đường tròn đường kính CB
hay B,E,F,C cùng thuộc một đường tròn(đpcm)
Tâm I của đường tròn ngoại tiếp tứ giác BEFC là trung điểm của CB
b) Ta có: BEFC là tứ giác nội tiếp(cmt)
nên \(\widehat{EFC}=\widehat{EBC}\)(Cùng nhìn cạnh EC)
\(\Leftrightarrow\widehat{KFC}=\widehat{KBE}\)
Xét ΔKFC và ΔKBE có
\(\widehat{FKB}\) chung
\(\widehat{KFC}=\widehat{KBE}\)(cmt)
Do đó: ΔKFC∼ΔKBE(g-g)
⇒\(\dfrac{KF}{KB}=\dfrac{KC}{KE}\)(Các cặp cạnh tương ứng tỉ lệ)
⇒\(KE\cdot KF=KB\cdot KC\)(đpcm)
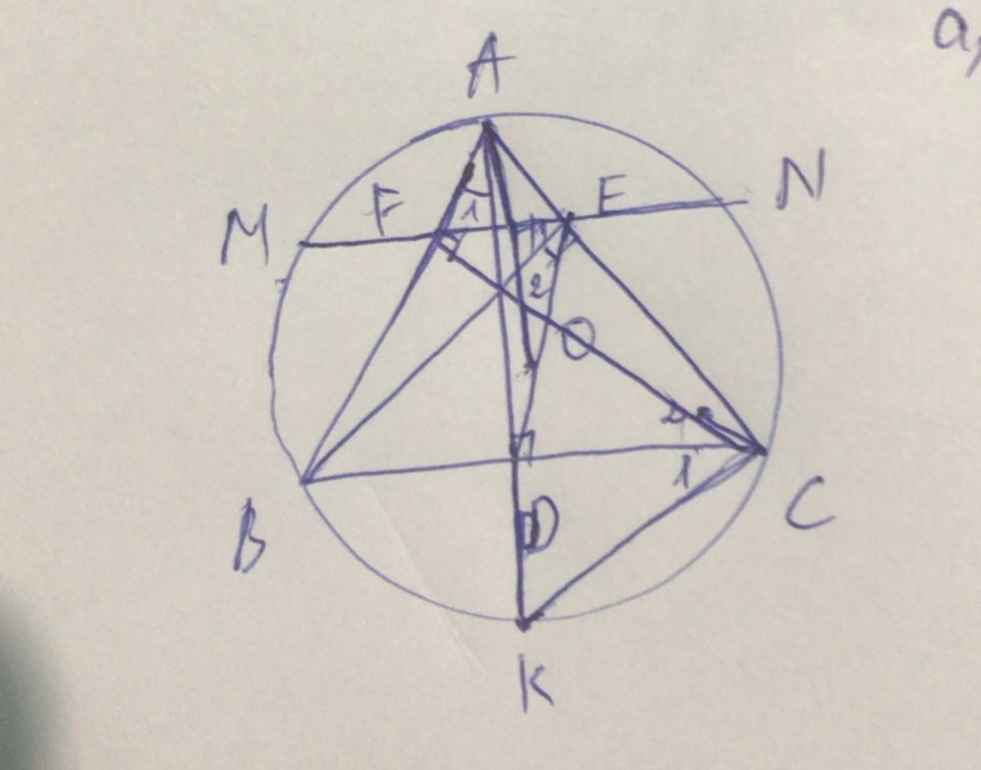



a, Xét tứ giác BCEF có
^CEB = ^CFB = 900
mà 2 góc này kề, cùng nhìn cạnh BC
Vậy tứ giác BCEF là tứ giác nt 1 đường tròn
b, Xét tứ giác AEHF có
^HEA = ^HFA = 900
Vậy tứ giác AEHF là tứ giác nt 1 đường tròn
c, Ta có ^AMN = ^ACN ( góc nt chắn cung AN )
^ANM = ^MBA ( góc nt chắn cung MA )
mà ^ACN = ^MBA ( tứ giác BCEF nt và 2 góc cùng nhìn cung CF )
=> ^AMN = ^ANM Vậy tam giác AMN cân tại A
=> AN = AM
d, Ta có : ^CBM = ^CFE ( góc nt chắn cung CE của tứ giác BCEF )
mặt khác : ^CNM = ^CBM ( góc nt chắn cung CM )
=> ^CFE = ^CNM, mà 2 góc này ở vị trí đồng vị )
=> MN // EF
e, Ta có AO là đường cao tam giác MAN
mà MN // EF ; AO vuông MN => AO vuông EF
4 năm nửa em mới TL dc