Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(hình bạn tự vẽ nhá :v )
a) Có goc BAC=90độ=>góc EAF=90độ
HE vuong goc voi AB =>góc HEA=90độ
HF vuong goc voi AC=>góc HFA=90độ
==>AEHF là hình chữ nhật
Có góc ABC=góc EHA
mà góc EHA= góc EFA
góc ABC+OAC=90 độ
=>góc OAC+góc AFE=90 độ =>OA vuông góc với EF
b)có góc PBA=góc PFA
góc APC=góc ABC
mà góc ABC= góc AFP
=>goca PBA= góc APE=>tam giác AEP đồng dạng vs APB (gg)
=>AP^2=AE.AB
mà AH^2=AE.AB
=>tam giac PAH cân
c)
Chứng minh tam giác DKC đồng dạng với tam giác DBA (g-g) , Suy ra DK.DA=DC.DB (1)
Chứng minh Tứ giác BEFC nội tiếp ( góc AEF = góc FCH cùng bắng với góc AHF )
Từ đó chứng minh hai tam giác DFC và DBE đồng dạng (g-g), Suy ra DF.DE=DC.DB (2)
Từ (1) và (2) suy ra DK.DA = DF.DE. Từ đó chứng minh tam giác DKF đồng dạng với DEA (theo trường hợp c-g-c)
Suy ra góc DKF = góc DEA
Suy ra tứ giác AEFK nội tiếp
d) chứng minh được OA vuông góc với PQ.
Suy ra cung AP=cung AQ. suy ra ˆADP=ˆACKADP^=ACK^
=> KFCD nội tiếp => ΔIFC∼ΔIDKΔIFC∼ΔIDK
=> IC.ID=IF.IK. rồi cm IH^2=IF.IK dựa vào tứ giác AKFH nội tiếp do tứ giác AEFK nội tiếp

a) Có goc BAC=90độ=>góc EAF=90độ
HE vuong goc voi AB =>góc HEA=90độ
HF vuong goc voi AC=>góc HFA=90độ
==>AEHF là hình chữ nhật
Có góc ABC=góc EHA
mà góc EHA= góc EFA
góc ABC+OAC=90 độ
=>góc OAC+góc AFE=90 độ =>OA vuông góc với EF
b)có góc PBA=góc PFA
góc APC=góc ABC
mà góc ABC= góc AFP
=>goca PBA= góc APE=>tam giác AEP đồng dạng vs APB (gg)
=>AP^2=AE.AB
mà AH^2=AE.AB
=>tam giac PAH cân
c)
Chứng minh tam giác DKC đồng dạng với tam giác DBA (g-g) , Suy ra DK.DA=DC.DB (1)
Chứng minh Tứ giác BEFC nội tiếp ( góc AEF = góc FCH cùng bắng với góc AHF )
Từ đó chứng minh hai tam giác DFC và DBE đồng dạng (g-g), Suy ra DF.DE=DC.DB (2)
Từ (1) và (2) suy ra DK.DA = DF.DE. Từ đó chứng minh tam giác DKF đồng dạng với DEA (theo trường hợp c-g-c)
Suy ra góc DKF = góc DEA
Suy ra tứ giác AEFK nội tiếp
d) chứng minh được OA vuông góc với PQ.
Suy ra cung AP=cung AQ. suy ra ˆADP=ˆACKADP^=ACK^
=> KFCD nội tiếp => ΔIFC∼ΔIDKΔIFC∼ΔIDK
=> IC.ID=IF.IK. rồi cm IH^2=IF.IK dựa vào tứ giác AKFH nội tiếp do tứ giác AEFK nội tiếp

a: góc AIH=góc AKH=góc KAI=90 độ
=>AIHK là hình chữ nhật
góc AKI+góc OAK
=góc AHI+góc OCA
=góc OBA+góc OCA=90 độ
=>AO vuông góc IK
b: Xét ΔAMB và ΔAIM có
góc ABM=góc AMI
góc MAB chung
=>ΔAMB đồng dạng với ΔAIM
=>AM/AI=AB/AM
=>AM^2=AI*AB
=>AM=AH
=>ΔAMH cân tại A

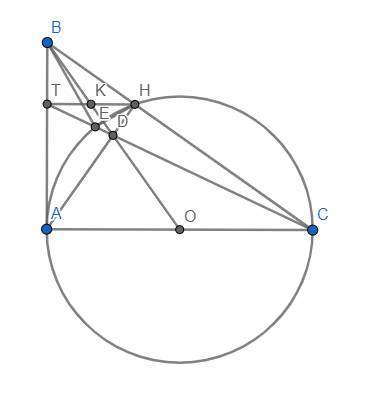
Gọi T là giao điểm của CD và AB. Khi đó xét tứ giác ACHT, ta có:
O (trung điểm AC), D (giao điểm của 2 đường chéo) và B (giao điểm của 2 đường thẳng chứa 2 cạnh đối) thẳng hàng nên ACHT là hình thang. (bổ đề hình thang quen thuộc)
\(\Rightarrow\) HT//AC \(\Rightarrow\) H, K, T thẳng hàng.
Lại có \(\widehat{CEH}=\widehat{CAH}\) (góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{CAH}=\widehat{B}\) (cùng phụ với góc C)
\(\Rightarrow\widehat{CEH}=\widehat{B}\)
\(\Rightarrow\) Tứ giác BTEH nội tiếp \(\Rightarrow\widehat{BEH}=\widehat{BTH}\)
Mà \(\widehat{BTH}=90^o\) nên \(\widehat{BEH}=90^o\). Ta có đpcm.
a: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
Xét tứ giác AIHK có \(\widehat{AIH}=\widehat{AKH}=\widehat{KAI}=90^0\)
nên AIHK là hình chữ nhật
Kẻ Ax là tiếp tuyến của (O) tại A
=>OA\(\perp\)Ax tại A
Xét ΔAHC vuông tại H có HK là đường cao
nên \(AK\cdot AC=AH^2\left(1\right)\)
Xét ΔAHB vuông tại H có HI là đường cao
nên \(AI\cdot AB=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AI\cdot AB=AK\cdot AC\)
=>\(\dfrac{AI}{AC}=\dfrac{AK}{AB}\)
Xét ΔAIK và ΔACB có
\(\dfrac{AI}{AC}=\dfrac{AK}{AB}\)
\(\widehat{IAK}\) chung
Do đó: ΔAIK~ΔACB
=>\(\widehat{AKI}=\widehat{ABC}\)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
=>\(\widehat{xAC}=\widehat{AKI}\)
mà hai góc này là hai góc ở vị trí so le trong
nên IK//Ax
=>OA\(\perp\)IK
b: ΔOMN cân tại O
mà OA là đường cao
nên OA là đường trung trực của MN
=>AM=AN
=>\(\widehat{AMN}=\widehat{ANM}\)
=>\(sđ\stackrel\frown{AM}=sđ\stackrel\frown{AN}\)
Xét (O) có
\(\widehat{AMN}\) là góc nội tiếp chắn cung AN
\(\widehat{ABM}\) là góc nội tiếp chắn cung AM
\(sđ\stackrel\frown{AM}=sđ\stackrel\frown{AN}\)
Do đó: \(\widehat{AMN}=\widehat{ABM}\)
Xét ΔAMI và ΔABM có
\(\widehat{AMI}=\widehat{ABM}\)
\(\widehat{MAI}\) chung
Do đó: ΔAMI~ΔABM
=>\(\dfrac{AM}{AB}=\dfrac{AI}{AM}\)
=>\(AM^2=AI\cdot AB\)
=>AM=AH
=>ΔAMH cân tạiA