Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải chi tiết:
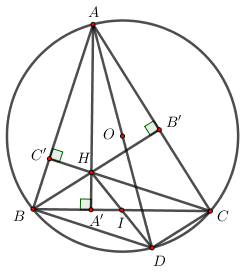
a) Chứng minh tứ giác AB’HC’ nội tiếp đường tròn.
Xét tứ giác AB’HC’ có ∠AB′H+∠AC′H=900+900=1800⇒∠AB′H+∠AC′H=900+900=1800⇒ Tứ giác AB’HC’ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Gọi I là giao điểm của hai đường thẳng HD và BC. Chứng minh I là trung điểm của đoạn BC.
Ta có ∠ABD=900∠ABD=900 (góc nội tiếp chắn nửa đường tròn) ⇒AB⊥BD⇒AB⊥BD.
Mà CH⊥AB(gt)⇒BD∥CHCH⊥AB(gt)⇒BD∥CH
Chứng minh tương tự ta có CD∥BHCD∥BH.
⇒⇒ Tứ giác BHCD là tứ giác nội tiếp (Tứ giác có các cặp cạnh đối song song)
Mà BC∩HD=I(gt)⇒IBC∩HD=I(gt)⇒I là trung điểm của BC.
c) Tính AHAA′+BHBB′+CHCC′AHAA′+BHBB′+CHCC′.
Ta có:
SHBCSABC=12HA′.BC12AA′.BC=HA′AA′⇒1−SHBCSABC=1−HA′AA′=AA′−HA′AA′=AHAA′SHBCSABC=12HA′.BC12AA′.BC=HA′AA′⇒1−SHBCSABC=1−HA′AA′=AA′−HA′AA′=AHAA′
Chứng minh tương tự ta có: BHBB′=1−SHACSABC;CHCC′=1−SHABSABCBHBB′=1−SHACSABC;CHCC′=1−SHABSABC
⇒AHAA′+BHBB′+CHCC′=1−SHBCSABC+1−SHACSABC+1−SHABSABC=3−SHBC+SHAC+SHABSABC=3−1=2⇒AHAA′+BHBB′+CHCC′=1−SHBCSABC+1−SHACSABC+1−SHABSABC=3−SHBC+SHAC+SHABSABC=3−1=2

Xét \(\Delta ABC\) và \(\Delta HBA\) có:
\(\widehat{BAC}=\widehat{BHA}=90^o\)
\(\widehat{B}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\) (1)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{HB}{AB}\) hay \(\dfrac{AB}{4+9}=\dfrac{4}{AB}\Rightarrow AB^2=52\Rightarrow AB=\sqrt{52}=2\sqrt{13}cm\)
Xét \(\Delta\text{A}BC\) và \(\Delta HAC\) có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{C}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g.g\right)\) (2)
Từ (1) và (2) \(\Rightarrow\Delta HAB\sim\Delta HCA\)
\(\Rightarrow\dfrac{AH}{HC}=\dfrac{HB}{AH}\) hay \(\dfrac{AH}{9}=\dfrac{4}{AH}\Rightarrow AH^2=36\Rightarrow AH=\sqrt{36}=6\left(cm\right)\)
Ta có \(\Delta ABC\) vuông tại A.
Áp dụng đinh lý Py-ta-go ta có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{\left(4+9\right)^2-\left(2\sqrt{13}\right)^2}=3\sqrt{13}cm\)
b) Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BC\cdot AH=\dfrac{1}{2}\cdot\left(4+9\right)\cdot6=39\left(cm^2\right)\)

a: tan B=3/4
=>AC/AB=3/4
=>AC=3cm
BC=căn 3^2+4^2=5cm
sin B=AC/BC=3/5
=>góc B=37 độ
=>góc C=53 độ
b: cos B=2/5
=>sin B=căn 21/5
=>AC/BC=căn 21/5
=>BC=50/căn 21(cm)
=>AB=20/căn 21(cm)
cos B=2/5
=>góc B=67 độ
=>góc C=23 độ
c: \(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>100-BC^2=6*8=48
=>BC=2*căn 13cm
\(\dfrac{AB}{sinC}=\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
=>2*căn 13/sin60=6/sinC=8/sinB
=>góc C=46 độ; góc B=180-60-46=74 độ


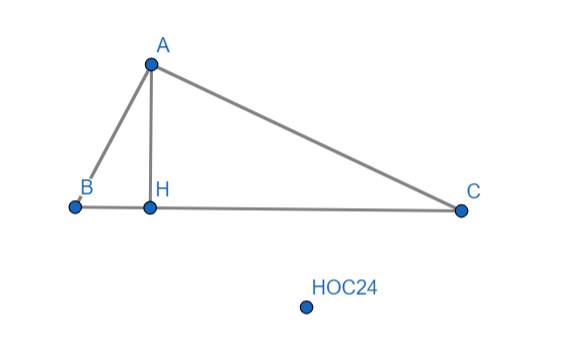
ta có
tan C=\(\frac{AH}{CH}\)
=> CH=\(\frac{AH}{\tan C}\)
CH=\(\frac{6}{\frac{2}{3}}=6.\frac{3}{2}=9\left(cm\right)\)
Xét tam giác AHC vuông tại H:
AH2+HC2=AC2 (py - ta -go)
AC2=62+92
AC2=117
=>AC=\(3\sqrt{13}\)(cm)
tan C = \(\frac{AB}{AC}\)
=>AB= tan C .AC
AB=\(\frac{2}{3}.3\sqrt{13}=2\sqrt{13}\)(cm)
Xét tam giác ABC vuông tại A:
AB2+AC2=BC2
\(\left(3\sqrt{13}\right)^2+\left(2\sqrt{13}\right)^2=BC^2\)
BC2=169
=>BC=13 (cm)

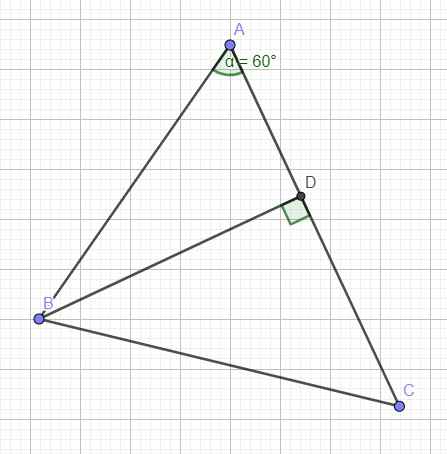
Kẻ đường cao BD ứng với AC
Trong tam giác vuông ABD:
\(\left\{{}\begin{matrix}cosA=\dfrac{AD}{AB}\\sinA=\dfrac{BD}{AB}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}AD=AB.cosA=8.cos60^0=4\\BD=AB.sinA=8.sin60^0=4\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow CD=AC-AD=8\)
Trong tam giác vuông BCD, áp dụng định lý Pitago:
\(BC=\sqrt[]{BD^2+CD^2}=4\sqrt{7}\) (cm)