Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta luôn chứng minh được rằng điểm M luôn nằm trong 3 góc của 1 tam giác

M đồngthời nằm trong hai góc BAC và góc ABC
=>M nằm trong ΔABC
=>M nằm trong góc BCA

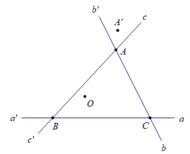
a. Giả sử ba đường thẳng aa’, bb’ và cc’ cắt nhau từng đôi một tại ba điểm A, B, C (hình vẽ). Điểm O cần vẽ là giao điểm của hai tia AO và BO sao cho tia AO nằm giữa hai tia AB và AC, tia BO nằm giữa hai tia BA và BC.
b. Điểm A’ nằm trên tia AA’ sao cho tia AA’ nằm giữa hai tia Ab’ và Ac, A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng BC.

â) vì 1 tia xuất phát từ đỉnh của 1 tam giác sẽ đi qua cách đối diện của đỉnh đó
nên BO cắt đoạn thẳng AC tại 1 điểm D nằm giữa A và C
b) ta có : BD đi qua điểm O ( O\(\in\)BD ) ( gt )
=> O nằm giữa hai điểm BD
c) vì OA , OB , OC là 3 tia xuất phát từ 3 đỉnh của một tam giác
nên 3 tia OA , OB ,ỐC ko có tia nào nằm giữa hai tia còn lại
CHÚC BẠN HỌC TỐT !!!