Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

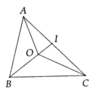
Vì OA=OB=OC
nên O là tâm đường tròn ngoại tiếp ΔABC
mà ΔABC đều
nên O là giao điểm của ba tia phân giác của các góc A,B,C

Ta có: AB < OA + OB (bất đẳng thức tam giác)
AC < OA + OC (bất đẳng thức tam giác)
BC < OB + OC (bất đẳng thức tam giác)
=> AB + AC + BC < 2 (OA + OB + OC) => \(\frac{AB+AC+BC}{2}< OA+OB+OC\)(1)
và OA + OB < BC + AC (kết quả của bài 17 SGK)
OB + OC < AB + AC (kết quả của bài 17 SGK)
OA + OC < AB + BC (kết quả của bài 17 SGK)
=> 2 (OA + OB + OC) < 2 (AB + AC + BC) => OA + OB + OC < AB + AC + BC (2)
Từ (1) và (2) => \(\frac{AB+AC+BC}{2}< OA+OB+OC< AB+AC+BC\)(đpcm)

a: Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
b: Ta có: ΔOAC=ΔOBC
nên AC=BC

Bài 1 :
Xét tam giác ABC và ADE có :
góc EAD = góc CAB (đối đỉnh)
CA=EA (gt)
BA=DA (gt)
suy ra tam giác ABC=ADE (c.g.c)
suy ra :DE =BC ( 2 cạnh tương ứng ) ; góc E= góc C ; góc D = góc B (các góc tương ứng )
Mà M; N lần lượt là trung điểm của DE và BC suy ra EN=DN=BM=CM
Xét tam giác ENA và CMA có:
EN = CM ( cmt)
góc E = góc C (cmt)
AE = AC (gt)
suy ra tam giác EAN = CMA (c.g.c) suy ra AM =AN ( 2 cạnh tương ứng )
Xét tam giác NDA và MBA có:
góc D= góc B (cmt)
ND = MB (cmt )
DA = BA (cmt )
suy ra tam giác NDA = MBA (c.g.c)suy ra góc NAD = góc MAB
Ta có góc DAC +MAC+MAB = 180 độ ( vì D nằm trên tia đối của tia AB )
Mà góc NAD = góc MAB suy ra góc DAC+MAC+NAD =180 độ
suy ra 3 điểm M,A,N thẳng hàng (2)
Từ (1) và (2 ) suy ra A là trung điểm của MN
( mình vẽ hình hơi xấu , mong bạn thông cảm . Nếu đúng nhớ kết bạn với mình nhé , mong tin bạn ^-^)

Bài 3:
Xét ΔHMB vuông tại H và ΔKMC vuông tại K có
MB=MC
\(\widehat{HMB}=\widehat{KMC}\)
Do đo: ΔHMB=ΔKMC
Suy ra: BH=CK

 tham khảo nha
tham khảo nha