Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cm: Xét t/giác ABH và t/giác ACH
có : AB = AC (gt)
\(\widehat{AHB}=\widehat{AHC}=90^0\) (gt)
AH : chung
=> t/giác ABC = t/giác ACH (ch - cgv)
=> BH = HC (2 cạnh t/ứng ) => AH là đường cao của t/giác ABC
=> \(\widehat{A_1}=\widehat{A_2}\) (2 góc t/ứng) => AH là đường p/giác của t/giác ABC
Ta có: BH = HC (cmt)
\(\widehat{AHB}=\widehat{AHC}=90^0\) (gt)
=> AH là đừng trung trực của t/giác ABC
b) Ta có: BH = HC = 1/2. BC = 1/2 . 8 = 4 (cm)
Áp dụng t/c của dãy tỉ số bằng nhau vào t/giác ABH vuông tại H , ta có:
AB2 = AH2 + BH2
=> AH2 = AB2 - BH2 = 52 - 42 = 25 - 16 = 9
=> AH = 3
Vậy AH = 3 cm
c) Xét t/giác ADH và t/giác AEH
có : \(\widehat{ADH}=\widehat{AEH}=90^0\) (gt)
AH : chung
\(\widehat{A_1}=\widehat{A_2}\) (gt)
=> t/giác ADH = t/giác AEH (ch - gn)
=> AD = AE (2 cạnh t/ứng)
=> t/giác ADE cân tại A
=> \(\widehat{D_1}=\widehat{E_1_{ }}=\frac{180^0-\widehat{A}}{2}\) (1)
Ta có: AB = AC (gt)
=> t/giá ABC cân tại A
=> \(\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\) (2)
Từ (1) và (2) => \(\widehat{D_1}=\widehat{B}\)
Mà 2 góc này ở vị trí đồng vị
=> DE // BC (Đpcm)

Xét hai tam giác vuông ΔABH ΔABH và ΔACH ΔACH:
Ta có: AH cạnh chung
AB=AC
Vậy ΔABH ΔABH = ΔACH ΔACH (c.g.c)
AH là đường cao đồng thời đường trung tuyến của ΔABC ΔABC cân tại A (AB=AC)
Vậy HC= HB hay H là trung điểm BC
2. BH = HC = BC2= 122 = 6BC2 = 122 = 6 cm
Áp dụng định lí Py-ta-go:
AH = √AB2 − HB2= √102 − 62 = 8AH = AB2− HB2 = 102− 62 = 8 cm
3. Ta có: AK là đường cao ΔAEH ΔAEH
Mà KE = KH nên AK cũng là đường trung tuyến ΔAEH ΔAEH
Vậy ΔAEH ΔAEH cân tại A
Nên AE=AH (1)
4. Ta có: AI là đường cao ΔADH ΔADH
Mà IH = ID nên AI cũng là đường trung tuyến ΔADH ΔADH
Vậy ΔAEH ΔAEH cân tại A
Nên AD = AH (2)
Từ (1)(2) Suy ra: AE=AD hay ΔAED ΔAED cân tại A
5. Xét ΔAEF ΔAEF và ΔADF ΔADF:
Ta có: AF cạnh chung
AE=AD
\(\widehat{AEF}\)=\(\widehat{ADF}\) \(\widehat{AEF}\)=\(\widehat{ADF}\)
Vậy ΔAEFΔAEF =ΔADFΔADF (c.g.c)
Nên EF = FD; AF là đường trung tuyến ΔAED ΔAED cân nên đồng thời đường cao nên AF vuông góc ΔAED ΔAED (3)
AF vuông góc BC (4)
Từ (3)(4) Suy ra: DE//BC
6. Để A là trung điểm ED thì ΔABC ΔABC vuông cân tại A
Giả sử ΔABC ΔABC vuông cân tại A nên AH=HB (đường cao đồng thời trung tuyến) IA=IB (đường cao đồng thời trung tuyến)
Tứ giác ADBH có hai đường chéo cắt nhau tại trung điểm mổi đường nên ADBH là hình bình hành
CM tương tự cho tứ giác AECH
Mà C,H,B thẳng hàng và HC=HB nên E,A,D thẳng hàng và A là trung điểm ED

a: Ta có: AH⊥BC
nên \(\widehat{AHB}=\widehat{AHC}=90^0\)
b: BH=CH=BC/2=4cm
=>AH=3cm
c: Xét ΔABM có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔABM cân tại B
d: Xét tứ giác ABMC có
H là trung điểm của AM
H là trung điểm của BC
Do đó: ABMC là hình bình hành
Suy ra: BM//AC

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng) và \(\widehat{BAH}=\widehat{CAH}\)(Hai góc tương ứng)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>góc BAH=góc CAH
=>AH là phân giác của góc BAC
c: BH=CH=3cm
AH=căn 5^2-3^2=4cm

a)
*Tính BC
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
a)
*Tính BE
Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)
Suy ra: BA=BE(hai cạnh tương ứng)
mà BA=6cm(gt)
nên BE=6cm
Vậy: BE=6cm

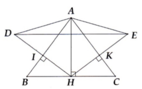



lỗi hình
lỗi ảnh