
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4: Áp dụng bất đẳng thức AM - GM, ta có: \(P=\text{}\Sigma_{cyc}a\sqrt{b^3+1}=\Sigma_{cyc}a\sqrt{\left(b+1\right)\left(b^2-b+1\right)}\le\Sigma_{cyc}a.\frac{\left(b+1\right)+\left(b^2-b+1\right)}{2}=\Sigma_{cyc}\frac{ab^2+2a}{2}=\frac{1}{2}\left(ab^2+bc^2+ca^2\right)+3\)Giả sử b là số nằm giữa a và c thì \(\left(b-a\right)\left(b-c\right)\le0\Rightarrow b^2+ac\le ab+bc\)\(\Leftrightarrow ab^2+bc^2+ca^2\le a^2b+abc+bc^2\le a^2b+2abc+bc^2=b\left(a+c\right)^2=b\left(3-b\right)^2\)
Ta sẽ chứng minh: \(b\left(3-b\right)^2\le4\)(*)
Thật vậy: (*)\(\Leftrightarrow\left(b-4\right)\left(b-1\right)^2\le0\)(đúng với mọi \(b\in[0;3]\))
Từ đó suy ra \(\frac{1}{2}\left(ab^2+bc^2+ca^2\right)+3\le\frac{1}{2}.4+3=5\)
Đẳng thức xảy ra khi a = 2; b = 1; c = 0 và các hoán vị
Bài 1: Đặt \(a=xc,b=yc\left(x,y>0\right)\)thì điều kiện giả thiết trở thành \(\left(x+1\right)\left(y+1\right)=4\)
Khi đó \(P=\frac{x}{y+3}+\frac{y}{x+3}+\frac{xy}{x+y}=\frac{x^2+y^2+3\left(x+y\right)}{xy+3\left(x+y\right)+9}+\frac{xy}{x+y}\)\(=\frac{\left(x+y\right)^2+3\left(x+y\right)-2xy}{xy+3\left(x+y\right)+9}+\frac{xy}{x+y}\)
Có: \(\left(x+1\right)\left(y+1\right)=4\Rightarrow xy=3-\left(x+y\right)\)
Đặt \(t=x+y\left(0< t< 3\right)\Rightarrow xy=3-t\le\frac{\left(x+y\right)^2}{4}=\frac{t^2}{4}\Rightarrow t\ge2\)(do t > 0)
Lúc đó \(P=\frac{t^2+3t-2\left(3-t\right)}{3-t+3t+9}+\frac{3-t}{t}=\frac{t}{2}+\frac{3}{t}-\frac{3}{2}\ge2\sqrt{\frac{t}{2}.\frac{3}{t}}-\frac{3}{2}=\sqrt{6}-\frac{3}{2}\)với \(2\le t< 3\)
Vậy \(MinP=\sqrt{6}-\frac{3}{2}\)đạt được khi \(t=\sqrt{6}\)hay (x; y) là nghiệm của hệ \(\hept{\begin{cases}x+y=\sqrt{6}\\xy=3-\sqrt{6}\end{cases}}\)
Ta lại có \(P=\frac{t^2-3t+6}{2t}=\frac{\left(t-2\right)\left(t-3\right)}{2t}+1\le1\)(do \(2\le t< 3\))
Vậy \(MaxP=1\)đạt được khi t = 2 hay x = y = 1

1. Ta có: \(x^2-2xy-x+y+3=0\)
<=> \(x^2-2xy-2.x.\frac{1}{2}+2.y.\frac{1}{2}+\frac{1}{4}+y^2-y^2-\frac{1}{4}+3=0\)
<=> \(\left(x-y-\frac{1}{2}\right)^2-y^2=-\frac{11}{4}\)
<=> \(\left(x-2y-\frac{1}{2}\right)\left(x-\frac{1}{2}\right)=-\frac{11}{4}\)
<=> \(\left(2x-4y-1\right)\left(2x-1\right)=-11\)
Th1: \(\hept{\begin{cases}2x-4y-1=11\\2x-1=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\y=-3\end{cases}}\)
Th2: \(\hept{\begin{cases}2x-4y-1=-11\\2x-1=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=3\end{cases}}\)
Th3: \(\hept{\begin{cases}2x-4y-1=1\\2x-1=-11\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-5\\y=-3\end{cases}}\)
Th4: \(\hept{\begin{cases}2x-4y-1=-1\\2x-1=11\end{cases}}\Leftrightarrow\hept{\begin{cases}x=6\\y=3\end{cases}}\)
Kết luận:...

thấy ngay \(p_6>2\text{ do đó: }VP\equiv1\left(\text{mod 8}\right)\text{ từ đó suy VP cũng đồng dư với 1 mod 8}\)
có bổ đề SCP LẺ chia 8 dư 1 do đó:
trong 5 số: \(p_1;p_2;...;p_5\text{ có 4 số chẵn; 1 số lẻ không mất tính tổng quát giả sử: }p_5\text{ lẻ}\Rightarrow16+p_5^2=p_6^2\text{(đơn giản)}\)
\(p+1=2a^2;p^2+1=2b^2\Rightarrow p\left(p-1\right)=2\left(b-a\right)\left(b+a\right)\)
\(\text{thấy ngay p lẻ}\Rightarrow UCLN\left(p^2+1,p+1\right)=1;\Rightarrow\left(a,b\right)=1\Rightarrow\left(b-a,a+b\right)=1\)
thấy ngay p>b-a nên: \(p=a+b;p-1=2a-2b\text{ hay:}a+b=2b-2a+1\Leftrightarrow3a=b+1\)
đến đây thì đơn giản

a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
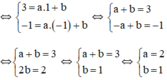
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.

a) Đồ thị hàm số y = ax + b đi qua A(1; 3) và B(-1; -1)
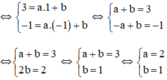
Vậy a = 2; b = 1; hàm số y = 2x + 1.
b) y = ax + b song song với y = x + 5
⇒ a = 1.
Đồ thị hàm số đi qua C(1; 2) ⇔ 2 = a.1 + b ⇔ a + b = 2 ⇒ b = 1.
Vậy a = 1; b = 1.

\(ab\left(a+b\right)=a^2+b^2-ab\Rightarrow ab=\dfrac{a^2+b^2-ab}{a+b}\)
\(A=\dfrac{a^3+b^3}{a^3b^3}=\dfrac{\left(a+b\right)\left(a^2+b^2-ab\right)}{a^3b^3}=\dfrac{\left(a+b\right)ab\left(a+b\right)}{a^3b^3}=\dfrac{\left(a+b\right)^2}{a^2b^2}\)
\(=\left(\dfrac{a+b}{ab}\right)^2=\left(\dfrac{a+b}{\dfrac{a^2+b^2-ab}{a+b}}\right)^2=\left(\dfrac{\left(a+b\right)^2}{a^2+b^2-ab}\right)^2\)
Ta có: \(a^2+b^2-ab>0;\forall a;b\ne0\Rightarrow\dfrac{\left(a+b\right)^2}{a^2+b^2-ab}\ge0\)
\(\dfrac{\left(a+b\right)^2}{a^2+b^2-ab}=\dfrac{a^2+b^2+2ab}{a^2+b^2-ab}=\dfrac{4\left(a^2+b^2-ab\right)-3\left(a^2+b^2-2ab\right)}{a^2+b^2-ab}=4-\dfrac{3\left(a-b\right)^2}{a^2+b^2-ab}\le4\)
\(\Rightarrow0\le\dfrac{\left(a+b\right)^2}{a^2+b^2-ab}\le4\)
\(\Rightarrow A\le16\)
\(A_{max}=16\) khi \(a=b=\dfrac{1}{2}\)

1.
Ta sẽ chứng minh BĐT sau: \(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}\ge\dfrac{10}{\left(a+b+c\right)^2}\)
Do vai trò a;b;c như nhau, ko mất tính tổng quát, giả sử \(c=min\left\{a;b;c\right\}\)
Đặt \(\left\{{}\begin{matrix}x=a+\dfrac{c}{2}\\y=b+\dfrac{c}{2}\end{matrix}\right.\) \(\Rightarrow x+y=a+b+c\)
Đồng thời \(b^2+c^2=\left(b+\dfrac{c}{2}\right)^2+\dfrac{c\left(3c-4b\right)}{4}\le\left(b+\dfrac{c}{2}\right)^2=y^2\)
Tương tự: \(a^2+c^2\le x^2\) ; \(a^2+b^2\le x^2+y^2\)
Do đó: \(A\ge\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{x^2+y^2}\)
Nên ta chỉ cần chứng minh: \(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{x^2+y^2}\ge\dfrac{10}{\left(x+y\right)^2}\)
Mà \(\dfrac{1}{\left(x+y\right)^2}\le\dfrac{1}{4xy}\) nên ta chỉ cần chứng minh:
\(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{x^2+y^2}\ge\dfrac{5}{2xy}\)
\(\Leftrightarrow\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{2}{xy}+\dfrac{1}{x^2+y^2}-\dfrac{1}{2xy}\ge0\)
\(\Leftrightarrow\dfrac{\left(x-y\right)^2}{x^2y^2}-\dfrac{\left(x-y\right)^2}{2xy\left(x^2+y^2\right)}\ge0\)
\(\Leftrightarrow\dfrac{\left(x-y\right)^2\left(2x^2+2y^2-xy\right)}{2x^2y^2}\ge0\) (luôn đúng)
Vậy \(A\ge\dfrac{10}{\left(a+b+c\right)^2}\ge\dfrac{10}{3^2}=\dfrac{10}{9}\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(\dfrac{3}{2};\dfrac{3}{2};0\right)\) và các hoán vị của chúng