Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta ABC\) có \(\widehat{B}=40^o,\widehat{A}=60^o\)
\(\Rightarrow\widehat{BCA}=80^o\)
Mà : CK là tia phân giác của góc \(\widehat{BCA}\)
\(\Rightarrow\widehat{BCK}=\widehat{ACK}=\frac{80^o}{2}=40^o\)
Xét \(\Delta BKC\) có : \(\widehat{KBC}=\widehat{KCB}=40^o\)
\(\Rightarrow\Delta BKC\) cân ở K
\(\Rightarrow KB=KC\) (đpcm)

2:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trực của AE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
=>ΔDAF=ΔDEC
=>DF=DC
c: AD=DE
DE<DC
=>AD<DC
d: Xét ΔBFC co BA/AF=BE/EC
nên AE//CF

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên BA=BE
=>ΔBAE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔBAE đều
c: Xét ΔABC vuông tại A có
\(\tan B=\dfrac{AC}{AB}\)
\(\Leftrightarrow AC=5\sqrt{3}\left(cm\right)\)
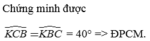
\(\widehat{ACB}=180^0-60^0-40^0=80^0\)
=>\(\widehat{KCB}=\dfrac{80^0}{2}=40^0\)
mà \(\widehat{KBC}=40^0\)
nên \(\widehat{KCB}=\widehat{KBC}\)
=>ΔKBC cân tại K
hay KB=KC