Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu a sai đề rồi bn
hok tốt
phải là tam giác OMQ = tam giác OPN chứ

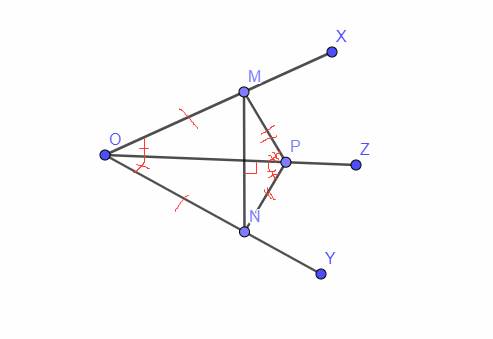
a) ta có \(OP+PQ=OQ\)
\(OM+MN=ON\)
mà \(OP=OM;PQ=MN\)
\(\Rightarrow OQ=ON\)
Xét \(\Delta NOPvà\Delta QOMcó\)
\(OP=OM\) ( giả thiết )
\(\widehat{QON}\) là góc chung
\(OQ=ON\) (chứng minh trên)
\(\Rightarrow\Delta NOP=\Delta QOM\left(c-g-c\right)\)
vậy \(\Delta NOP=\Delta QOM\)
b) tự làm nhé

#\(N\)
`a,` Xét Tam giác `OMP` và Tam giác `ONP` có:
`OM = ON (g``t)`
\(\widehat{MOP}=\widehat{NOP}\) `(` tia phân giác \(\widehat{xOy}\) `)`
`OP` chung
`=>` Tam giác `OMP =` Tam giác `ONP (c-g-c)`
`b,` Vì Tam giác `OMP =` Tam giác `ONP (a)`
`=> MP = NP (` 2 cạnh tương ứng `)`
`=>`\(\widehat{MPH}=\widehat{NPH}\) `(` 2 góc tương ứng `)`
Xét Tam giác `MPH` và Tam giác `NPH` có:
`MP = NP (CMT)`
\(\widehat{MPH}=\widehat{NPH}(CMT)\)
`PH` chung
`=>` Tam giác `MPH = `Tam giác `NPH (c-g-c)`
`=>`\(\widehat{MHP}=\widehat{NHP}\) `(` 2 góc tương ứng `)`
Mà `2` góc này ở vị trí kề bù
`=>`\(\widehat{MHP}+\widehat{NHP}=180^0\)
`=>` \(\widehat{MHP}=\widehat{NHP}=\)\(\dfrac{180}{2}=90^0\)
`=>`\(MN\perp OP\left(đpcm\right)\)

Cho góc xOy nhọn, Ot là phân giác, trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA = OB, trên Ot lấy điểm H sao cho OH > OA. a) Chứng minh tam giác OHA = tam giác OHB. b) Tia AH cắt Oy tại M, tia BH cắt Ox tại N. Chứng minh tam giác OAM = tam giác OBN. c) Chứng minh AB vuông góc OH - Toán học Lớp 7 - Bài tập Toán học Lớp 7 - Giải bài tập Toán học Lớp 7 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
Songoku Sky FC làm đúng rồi đó
Cho xoy nhọn , ot là tác phẩm .........
ai thấy đúng thì tk nhé
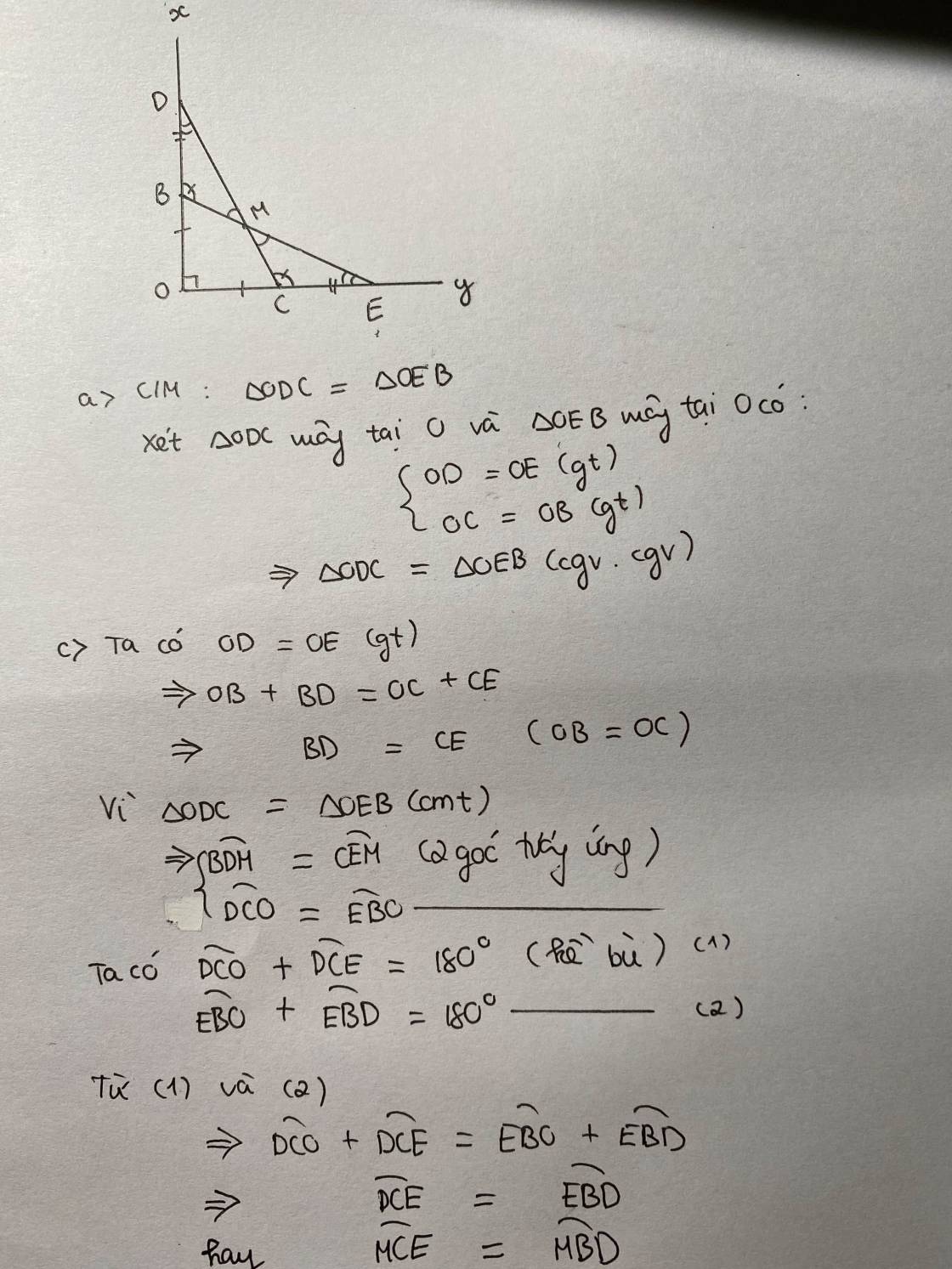

a) Xét 2 tam giác OPN và OMQ có:
OM=OP (GT)
Góc O chung
PQ=MN(GT)
=> tam giác OPN = tam giác OMQ (c.g.c)
a/ Xét t/g OPN và t/g OMQ có:
OP = OM (gt)
\(\widehat{O}:chung\)
ON = OQ (gt)
=> t/g OPN = t/g OMQ (c.g.c)(đpcm)
b/ Xét t/g MPN và t/g PMQ có:
MN = PQ (gt)
MP: cạnh chung
PN = MQ (2 cạnh tương ứng do t/g OPN = t/g OMQ)
=> t/g MPN = t/g PMQ (c.c.c)(đpcm)
c/ Ta có:
\(\widehat{OPI}+\widehat{IPQ}=180^o\) (kề bù)
\(\widehat{OMI}+\widehat{IMN}=180^o\) (kề bù)
mà \(\widehat{OPI}=\widehat{OMI}\) (2 góc tương ứng do t/g OPN = t/g OMQ)
=> \(\widehat{IMN}=\widehat{IPQ}\)
Xét t/g IMN và t/g IPQ có:
\(\widehat{INM}=\widehat{IQP}\) (đã cm)
MN = PQ (gt)
\(\widehat{IMN}=\widehat{IPQ}\left(cmt\right)\)
=> t/g IMN = t/g IPQ (g.c.g)(đpcm)