Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABH vuông tại H và ΔDBH vuông tại H có
BH chung
HA=HD(gt)
Do đó: ΔABH=ΔDBH(hai cạnh góc vuông)
Suy ra: \(\widehat{ABH}=\widehat{DBH}\)(hai góc tương ứng)
mà tia BH nằm giữa hai tia BA,BD
nên BH là tia phân giác của \(\widehat{ABD}\)(đpcm)
b) Xét ΔACH vuông tại H và ΔDCH vuông tại H có
CH chung
AH=DH(gt)
Do đó: ΔACH=ΔDCH(hai cạnh góc vuông)
Suy ra: CA=CD(hai cạnh tương ứng)
Ta có: ΔABH=ΔDBH(cmt)
nên BA=BD(hai cạnh tương ứng)
Xét ΔABC và ΔDBC có
BA=BD(cmt)
BC chung
CA=CD(cmt)
Do đó: ΔABC=ΔDBC(c-c-c)

M A B C N H F D
a) Xét \(\Delta\)AHB và \(\Delta\)DHB có:
^AHB = ^DHB ( 1v )
HA = HD ( giả thiết )
MH chung
=> \(\Delta\)AHB = \(\Delta\)DHB ( c.g.c)
b) Từ (a) => ^ABH = ^DHB => BH là phân giác ^ABD
Vì \(\Delta\)ABC nhọn => H nằm trong đoạn BC
=> BC là phân giác ^ABD
c) NF vuông BC
AH vuông BC
=> NF // AH
=> ^NFM = ^HAM ( So le trong )
Lại có: ^HMA = NMF ( đối đỉnh ) và MA = MF ( giả thiết )
=> \(\Delta\)NFM = \(\Delta\)HAM ( g.c.g)
=> NF = AH ( 2)
Từ ( a) => AH = HD ( 3)
Từ (2) ; (3) => NF = HD

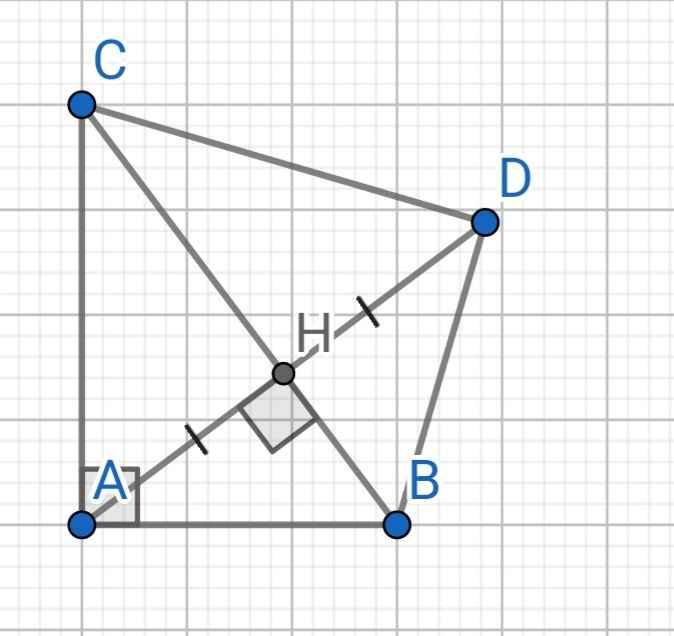 a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:
a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:
BH là cạnh chung
HA = HD (gt)
⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)
⇒ ∠ABH = ∠DBH (hai góc tương ứng)
⇒ BH là tia phân giác của ∠ABD
b) Do ∆ABH = ∆DBH (cmt)
⇒ AB = DB (hai cạnh tương ứng)
Do ∠ABH = ∠DBH (cmt)
⇒ ∠ABC = ∠DBC
Xét ∆ABC và ∆DBC có:
AB = DB (cmt)
∠ABC = ∠DBC (cmt)
AC là cạnh chung
⇒ ∆ABC = ∆DBC (c-g-c)
c) Do ∆ABC = ∆DBC (cmt)
⇒ ∠BAC = ∠BDC = 90⁰ (hai góc tương ứng)
⇒ BD ⊥ CD

a: Xét ΔCAD có
CH vừa là đường cao, vừa là trung tuyến
=>ΔCAD cân tại C
b: Xet ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
=>ΔCAB=ΔCDB

a: Xét ΔCAD có
CH vừa là đường cao, vừa là trung tuyến
=>ΔCAD cân tại C
b: Xet ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
=>ΔCAB=ΔCDB

A B C D H
a) Xét \(\Delta BHA\) và \(\Delta BHD\) có:
- BH là cạnh chung
- \(\widehat{BHA}=\widehat{BHD}\) (\(\widehat{BHA}=90^o\) mà \(\widehat{BHA}\) và \(\widehat{BHD}\) kề bù => \(\widehat{BHD}=90^o=\widehat{BHA}\))
- AH=HD (giả thiết đề bài)
=>\(\Delta BHA\)=\(\Delta BHD\) (c.g.c) => \(\widehat{HBA}=\widehat{HBD}\) (2 góc tương ứng) => BC là tia phân giác của góc BAD
b) Xét \(\Delta ABC\) và \(\Delta DBC\) có:
- AB=BD (vì \(\Delta BHA\)= mà AB và BD là 2 cạnh tương ứng)
- (vì = mà và là 2 góc tương ứng)
- BC là cạnh chung
=>\(\Delta ABC\) =\(\Delta DBC\) ( c.g.c)
Vậy bài toán đã được chứng minh.

a: Xét ΔAHB vuông tại H và ΔDHB vuông tại H có
BH chung
HA=HD
Do đó: ΔAHB=ΔDHB
b: Ta co: ΔAHB=ΔDHB
nên góc ABH=góc DBH
=>BH là phân giác của góc ABD
Ta có: ΔBAD cân tại B
mà BC là đường cao
nên BC là trung trực của AD
c: Xét ΔABC và ΔDBC có
BA=BD
góc ABC=góc DBC
BC chung
Do đó: ΔABC=ΔDBC