Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét ΔCBD có :
CI = IB
CO = OD (bán kính)
⇒ BD // OI (OI là đường trung bình của tam giác BCD).
Vậy BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:
AC^2 = OA^2 – OC^2 = 42 – 22 = 12
=> AC = √12 = 2√3 (cm)
\(\sin OAC=\frac{OC}{OA}=\frac{1}{2}\)
=> OAC =30 độ
mà BAC =2OAC
=. BAC =60
Tam giác ABC cân có BAC = 60 => Tam giác ABC đều
+> AB=AC=BC=2√3 (cm)
K cho mk nh
câu A : AB = AC ( theo tính chất của đường tiếp tuyến ) suy ra : tam giác ABC cân tại A , OA là đường phân giác cũng là đường cao vậy OA vuông góc với BC

Ta có
DB=DM; EC=EM; AB=AC (2 tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến các tiếp điểm = nhau)
\(C_{ADE}=AD+DM+AE+EM=AD+DB+AE+EC=\)
\(=AB+AC=2AB\)

Tam giác ABC vuông tại A (theo định lý Py-ta-go đảo)
⇒AC⊥AB,⇒AC⊥AB, do đó AC là tiếp tuyến.
Ta có: AB2 + AC2 = 32 + 42 = 25.
BC2 = 52 = 25.
Nên AB2 + AC2 = BC2.
Suy ra tam giác ABC vuông tại A hay AC ⊥ BA.
Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn.

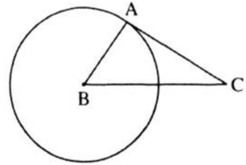
Ta có: AB2 + AC2 = 32 + 42 = 25
BC2 = 52 = 25
Nên AB2 + AC2 = BC2
=> tam giác ABC vuông tại A hay AC ⊥ BA.
Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn.

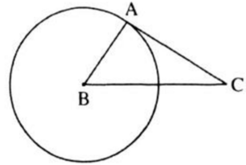
Ta có: A B 2 + A C 2 = 3 2 + 4 2 = 25 B C 2 = 5 2 = 25
Nên A B 2 + A C 2 = B C 2
=> tam giác ABC vuông tại A hay AC ⊥ BA.
Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn.

a: ΔOAB cân tại O
mà OC là đường cao
nên OC là phân giác của \(\widehat{AOB}\)
Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>\(\widehat{OAC}=\widehat{OBC}=90^0\)
=>CB là tiếp tuyến của (O)
b: Gọi giao điểm của AB với OC là H
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>HA=HB=12(cm)
ΔAHO vuông tại H
=>\(HA^2+HO^2=AO^2\)
=>\(HO^2=15^2-12^2=81\)
=>HO=9(cm)
Xét ΔOAC vuông tại A có AH là đường cao
nên OH*OC=OA^2
=>OC=15^2/9=25(cm)

Vẽ OM⊥AB⇒OM⊥CD.
Xét đường tròn (O;OC) (đường tròn nhỏ) có OM là một phần đường kính, CD là dây và OM⊥CD nên M là trung điểm của CD hay MC=MD (định lý)
Xét đường tròn (O;OA) (đường tròn lớn) có OM là một phần đường kính, AB là dây và OM⊥AB nên M là trung điểm của AB hay MA=MB (định lý)
Ta có MA=MB và MC=MD (cmt) nên trừ các đoạn thẳng theo vế với vế ta được MA−MC=MB−MD ⇒AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.

a, Tam giác ABC ngọi tiếp đường tròn \(\left(O\right)\)nên AB, BC, AC lần lượt là tiếp tuyến tại D, E , F của đường tròn.
Theo tính chất của hai đường tiếp tuyến cắt nhau, ta có:
AD = AF ; DB = BE ; FC = CE
Xét vế phải:
VP = AB + AC - BC
= ( AD + DB ) + ( AF + CF ) - ( BE + CE )
Thay DB = BE , FC = CE vào biểu thức trên, ta được:
VP = ( AD + BE ) + ( AF + CE ) - ( BE + CE )
= AD + BE + AF + CE - BE - CE
= ( AD + AF ) + ( BE - BE ) + ( CE - CE )
= AD + AF
= AD + AD = 2AD
Vậy 2AD = AB + AC - BC
b, Các hệ thức tương tự là:
2BD = BA + BC - AC
2CF = CA + CB - AB
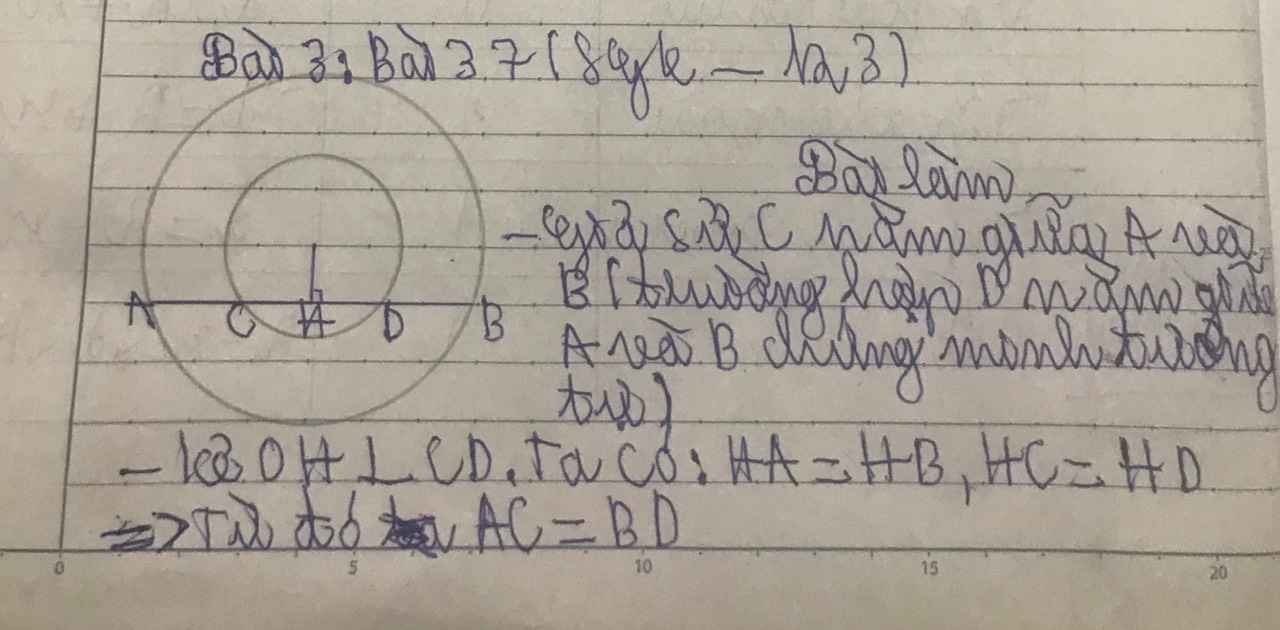

Tam giác ABCABC có:
AB^2+AC^2=3^{2}+4^{2}=5^{2}AB2+AC2=32+42=52
Mặt khác: BC^{2}=5^{2}BC2=52
Vậy \mathrm{AB}^{2}+\mathrm{AC}^{2}=\mathrm{BC}^{2}AB2+AC2=BC2.
Do đó \widehat{BAC}=90^{\circ}BAC=90∘ (định lí Py-ta-go đảo).
CACA vuông góc với bán kính BABA tại AA nên CACA là tiếp tuyến của đường tròn (B)(B).
tam giác ABC