K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 9 2021
Bài 6:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
Ta có: \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2}{x-\sqrt{x}}\right):\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{x+2}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)
\(=\dfrac{x+2}{\sqrt{x}}\)
b: Thay \(x=3-2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3-2\sqrt{2}+2}{\sqrt{2}-1}=\dfrac{5-2\sqrt{2}}{\sqrt{2}-1}=3\sqrt{2}+1\)
26 tháng 9 2021
Bài 5:
a: Ta có: \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}+1}\)
\(=\dfrac{x-1}{\sqrt{x}}\)
b: Để P<0 thì x-1<0
hay x<1
Kết hợp ĐKXĐ, ta được: 0<x<1
20 tháng 3 2023
3:
1: Đặt căn x-3=a; |2y-1|=b
Theo đề, ta có: 8/a+1/b=5 và 4/a+1/b=3
=>a=2 và b=1
=>căn x=5 và |2y-1|=1
=>x=25 và \(y\in\left\{1;0\right\}\)
2:
mx-2y=2m và -2x+y=m+1
=>mx-2y=2m và -4x+2y=2m+2
=>(m-4)x=4m+2 và y=-2x-m-1
=>x=(4m+2)/(m-4) và \(y=\dfrac{-8m-4}{m-4}-m-1\)
x=y
=>\(\dfrac{4m+2}{m-4}=\dfrac{-8m-4}{m-4}-m-1\)
=>\(\dfrac{4m+2+8m+4}{m-4}=-m-1\)
=>(m-4)(-m-1)=12m+6
=>-m^2-m+4m+4-12m-6=0
=>-m^2-9m-2=0
=>\(m=\dfrac{-9\pm\sqrt{73}}{2}\)
1 tháng 11 2021
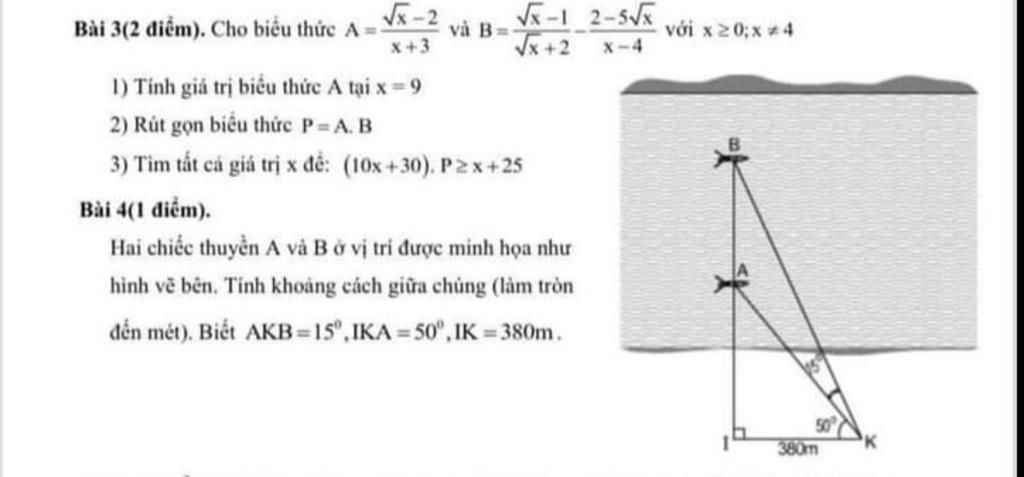
Bài 3:
a: Thay x=9 vào A, ta được:
\(A=\dfrac{3-2}{3+3}=\dfrac{1}{6}\)
QN
0
5 tháng 9 2021
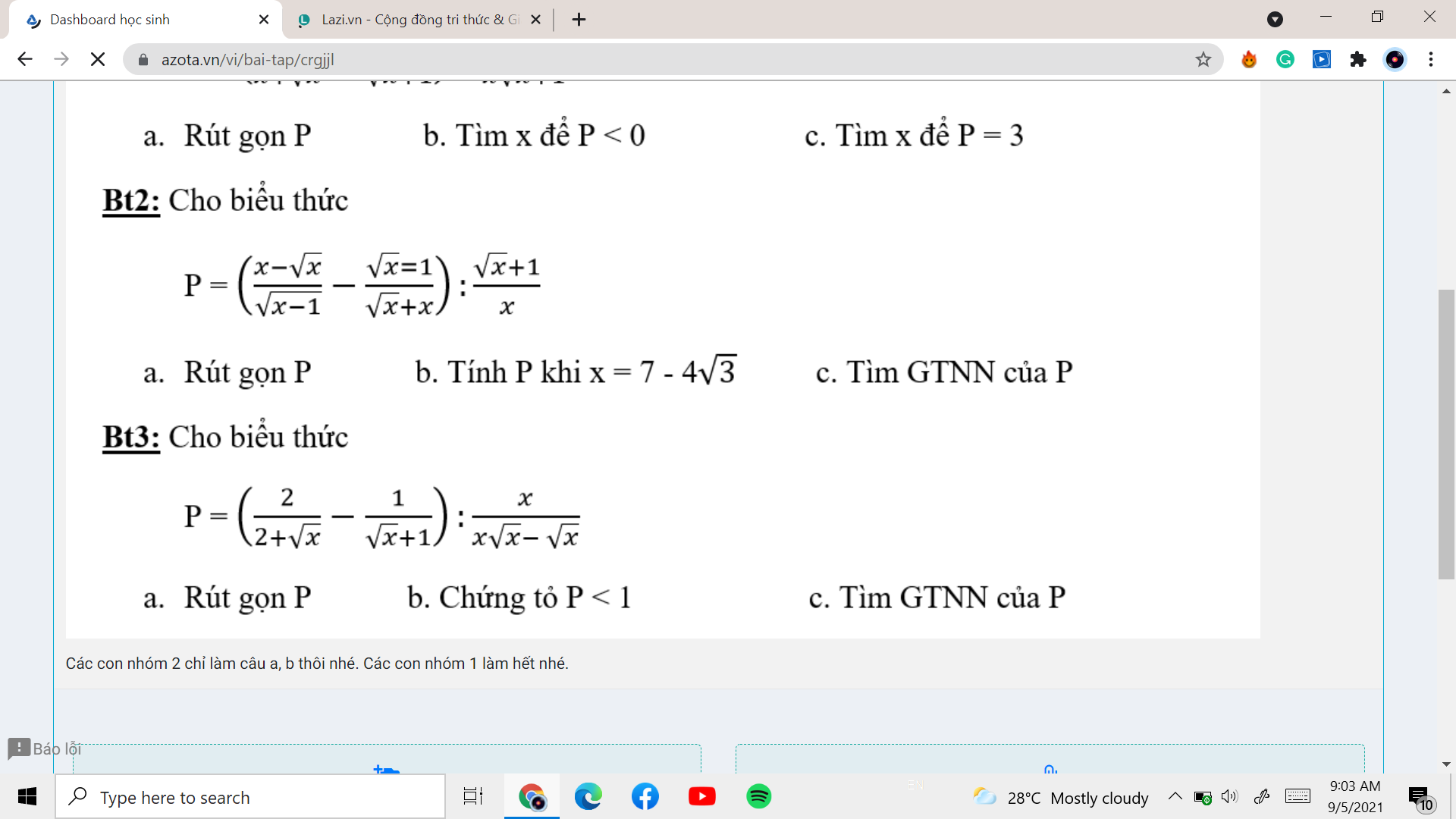
Bài 3:
a: Ta có: \(P=\left(\dfrac{2}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{x}{x\sqrt{x}-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}+2-\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{x}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
7 tháng 10 2021
Bài 2:
Xét ΔABC vuông tại C có
\(CB=BA\cdot\sin60^0=12\cdot\dfrac{\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\)
T
1
2 tháng 1 2022
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB
17 tháng 9 2021
\(\sqrt{9x+9}-2\sqrt{\dfrac{x+1}{4}}=4\left(đk:x\ge-1\right)\)
\(\Leftrightarrow3\sqrt{x+1}-\sqrt{x+1}=4\)
\(\Leftrightarrow2\sqrt{x+1}=4\)
\(\Leftrightarrow\sqrt{x+1}=2\Leftrightarrow x+1=4\Leftrightarrow x=3\left(tm\right)\)
Bài 3:
Ta có: \(\sqrt{4x^2-12x+9}=4\)
\(\Leftrightarrow\left|2x-3\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=4\\2x-3=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=7\\2x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Bài 2:
a: Ta có: \(\sqrt{17-3\sqrt{32}}+\sqrt{17+3\sqrt{32}}\)
\(=\sqrt{17-12\sqrt{2}}+\sqrt{17+12\sqrt{2}}\)
\(=3-2\sqrt{2}+3+2\sqrt{2}\)
=6
b: Ta có: \(\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\)
\(=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}\)
\(=2\sqrt{2}\)