Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu là kết quả của việc chọn ngẫu nhiên 4 con trong số 52 con
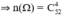
a. Đặt A : « Cả 4 con lấy ra đều là át »
⇒ n(A) = 1
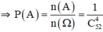
b. + B : « Không có con át nào trong 4 con khi lấy ra »
⇒ B là kết quả của việc chọn ngẫu nhiên 4 con trong số 48 con còn lại
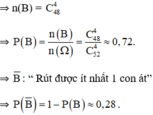
c. C: “Rút được 2 con át và 2 con K”.
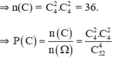

Phép thử T được xét là: "Từ cỗ bài tú lơ khơ 52 con bài, rút ngẫu nhiên 4 con bài".
Mỗi kết quả có thể có là một tổ hợp chập 4 của 52 con bài. Do đó số các kết quả có thể có của phép thử T là n(Ω) = C452 = = 270725.
Vì rút ngẫu nhiên nên các kết quả có thể có là đồng khả năng.
a) Gọi biến cố A: "Rút được bốn con át". Ta có, số kết quả có thể có thuận lợi cho A là n(A) = 1. Suy ra P(A) = ≈ 0,0000037.
b) Gọi biến cố B: "Rút được ít nhất một con át". Ta có
= "Rút được 4 con bài đều không là át". Mỗi kết quả có thể thuận lợi cho
là một tổ hợp chập 4 của 48 con bài không phải là át. Suy ra số các kết quả có thể có thuận lợi cho
là C448 =
= 194580. Suy ra P(
) =
≈ 0,7187.
Qua trên ta có P(B) = 1 - P() ≈ 0,2813.
c) Gọi C là biến cố: "Rút được hai con át và hai con K".
Mỗi kết quả có thể có thuận lợi cho C là một tổ hợp gồm 2 con át và 2 con K. Vận dụng quy tắc nhân tính được số các kết quả có thể có thuận lợi cho C là
n(C) = C24 C24 = 6 . 6 = 36.
Suy ra P(C) = ≈ 0,000133.

Không gian mẫu: \(n(\Omega)=C^3_{52}=22100\)
Rút được 2 con K từ 4 con: \(C^2_4=6\)
Rút con còn lại từ 52-4=48 (lá còn lại): \(C_{48}^1=48\)
\(\Rightarrow n\left(A\right)=6.48=288\)
\(\Rightarrow p\left(A\right)=\dfrac{288}{22100}=\dfrac{72}{5525}\)

Kí hiệu A k : Lần thứ k lấy được con át , k ≥ 1 . Rõ ràng A 1 , A 2 độc lập.
a) Ta cần tính P ( A 1 ∩ A 2 ) .
Ta có:
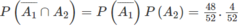
b) Theo bài ra ta cần tính:
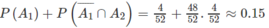

Chọn B
Xếp 9 người vào 9 ghế kê hàng ngang ta có: Ω =9! cách sắp xếp.
Gọi B là biến cố để “mỗi thầy giáo ngồi giữa 2 học sinh và học sinh A ngồi ở một trong hai đầu hàng.”
Theo đề, học sinh A ngồi ở một trong hai đầu hàng nên có 2 cách sắp xếp.
Xếp 5 học sinh còn lại vào 5 vị trí có 5! cách sắp xếp. Xem mỗi học sinh tạo thành một vách ngăn tạo thành 5 khoảng trống. Xếp 3 thầy vào 5 khoảng trống có A 5 3 cách.
![]() cách.
cách.
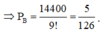

Chọn B
Số phần tử của không gian mẫu là: 13!
Gọi A là biến cố: “Thầy giáo đứng giữa 2 học sinh nam”
Bước 1: Xếp hai học sinh nam đứng cạnh thầy giáo có A 8 2 .
Coi hai học sinh nam đứng cạnh thầy giáo và thầy giáo là một người.
Bước 2: Xếp 12 người quanh một bàn tròn có 11! cách.
Số kết quả thuận lợi của biến cố A là: A 8 2 .11!
Vậy 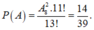

Ta có số cách chọn ngẫu nhiên 4 quân bài là: C 52 4 = 270725
Suy ra Ω = 270725
Vì bộ bài chỉ có 1 tứ quý K nên ta có Ω A = 1
Vậy P ( A ) = 1 270725
Đáp án A

Không gian mẫu: \(C_{52}^2\)
a. Lấy hai quân 2 (từ 4 quân 2) có \(C_4^2\) cách
Xác suất: \(P=\dfrac{C_4^2}{C_{52}^2}=...\)
b. Lấy 1 con 2 và một con Át có: \(C_4^1.C_4^1=16\) cách
Xác suất: \(P=\dfrac{16}{C_{52}^2}=...\)
c. Lấy ra 2 quân trong đó không có quân Át nào: \(C_{48}^2\) cách
\(\Rightarrow\) Có \(C_{52}^2-C_{48}^2\) cách lấy 2 con có ít nhất 1 con Át
Xác suất: \(P=\dfrac{C_{52}^2-C_{48}^2}{C_{52}^2}=...\)