Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

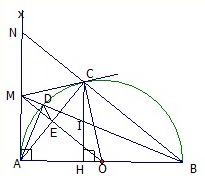
a, Sử dụng tỉ số lượng giác trong tam giác vuông ∆AMO ta tính được A O M ^ = 60 0
b, Tính được A O B ^ = 120 0 , sđ A B C ⏜ = 120 0
c, Ta có A O C ⏜ = B O C ⏜ => A C ⏜ = B C ⏜

Hình tự vẽ nha
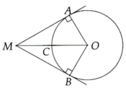
1, Ta có: MA = MC (t/c 2 tt cắt nhau)
OA = OC (t/c 2 tt cắt nhau)
=> OM là đường trung trực của AC
=> OM _|_ AC hay \(\widehat{OEC}=90^o\)
Có: \(\widehat{OBD}=90^o\) (t/c tt của đường tròn)
XÉt tứ giác OBDE có: \(\widehat{OEC}+\widehat{OBD}=90^o+90^o=180^o\)
Mà 2 góc này ở vị trí đối diện
=> tứ giác OBDE nội tiếp (đpcm)
2, Xét t/g ABC có: góc ACB là góc nội tiếp chắn nửa đường tròn
=> \(\widehat{ACB}=90^o\) hay BC _|_ AD
Áp dụng hệ thức b2=a.b' vào t/g ABD vuông tại B, đường cao BC có: \(AC.AD=AB^2=\left(2R\right)^2=4R^2\) (vì AB là đường kính) (đpcm)
3, Gọi K là trung điểm của MF (K thuộc MF) => KM=KF
Ta có: AM _|_ AB (t/c tt) ; BF _|_ AB (t/c tt) (1)
=> AM // BF => tứ giác AMBF là hình thang
Xét hình thang AMBF có: KM = KF ; OA = OB (gt)
=> OK là đường trung bình của hình thang AMBF
=> OK // AM // BF mà AM _|_ AB (cmt)
=> OK _|_ AB (1)
Lại có: t/g MOF nội tiếp đường tròn => O thuộc tròn ngoại tiếp t/g MOF (2)
Từ (1) và (2) => đpcm

Bài 1:
a,
OM là đường trung bình của tam giác BAC => OM = 1/2*BC
OM = 1/2*AB
=> AB=BC (đpcm).
b,
Tam giác ABC đều => BC = 2*r(O)
MN là đường trung bình của tam giác ABC => MN = 1/2*AB = r(O) = OM = OB =BN => BOMN là hình thoi.