Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Thay x=-1 và y=-2 vào y=(m-1)x+2m, ta được:
\(-\left(m-1\right)+2m=-2\)
=>2m-m+1=-2
=>m+1=-2
=>m=-3
b: Khi m=-1 thì \(y=\left(-1-1\right)x+2\cdot\left(-1\right)=-2x-2\)

Bạn nhập lại hai hàm số đó nhé chính giữa mik không biết là dấu + hay -

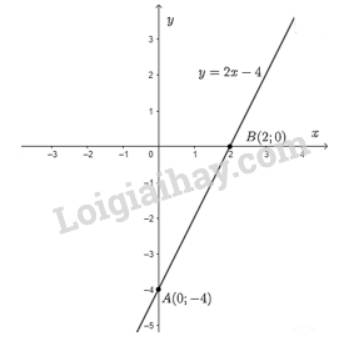
a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).

Đáp án đúng là D
- Đồ thị hàm số \(y = \dfrac{1}{3}x + 2\) là đường thẳng có hệ số góc là \(a = \dfrac{1}{3}\).
- Đồ thị hàm số \(y = - \dfrac{1}{3}x + 2\) là đường thẳng có hệ số góc là \(a = - \dfrac{1}{3}\).
- Đồ thị hàm số \(y = - 3x + 2\) là đường thẳng có hệ số góc là \(a = - 3\).
Vì cả ba đường thẳng đều có hệ số góc khác nhau nên chúng cắt nhau.
- Đồ thị hàm số \(y = \dfrac{1}{3}x + 2\) cắt trục tung tại điểm \(A\left( {0;2} \right)\).
- Đồ thị hàm số \(y = - \dfrac{1}{3}x + 2\) cắt trục tung tại điểm \(A\left( {0;2} \right)\)
- Đồ thị hàm số \(y = - 3x + 2\) cắt trục tung tại điểm \(A\left( {0;2} \right)\)
Do đó điểm \(A\left( {0;2} \right)\) là giao điểm của ba đồ thị hàm số.
Vậy đồ thị của các hàm số trên là các đường thẳng cắt nhau tại một điểm.

b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+2\)
\(\Leftrightarrow x^2-2x-8=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{1}{4}\cdot4^2=4\\y=\dfrac{1}{4}\cdot\left(-2\right)^2=1\end{matrix}\right.\)

Lời giải:
a. Vì đths đi qua $A(-2;3)$ nên:
$y_A=(2m+5)x_A-1$
$\Rightarrow 3=(2m+5)(-2)-1\Rightarrow m=\frac{-7}{2}$
b. ĐTHS sau khi tìm được $m$ có pt: $y=-2x-1$. Bạn có thể tự vẽ
c. ĐTHS cắt trục hoành tại điểm có hoành độ -3, tức là đi qua điểm $(-3,0)$
$\Rightarrow 0=(2m+5)(-3)-1$
$\Rightarrow m=\frac{-8}{3}$

a)
- Với \(x = - 2 \Rightarrow f\left( { - 2} \right) = - 2;g\left( { - 2} \right) = - 2 + 3 = 1\);
- Với \(x = - 1 \Rightarrow f\left( { - 1} \right) = - 1;g\left( { - 1} \right) = - 1 + 3 = 2\);
- Với \(x = 0 \Rightarrow f\left( 0 \right) = 0;g\left( 0 \right) = 0 + 3 = 3\);
- Với \(x = 1 \Rightarrow f\left( 1 \right) = 1;g\left( 1 \right) = 1 + 3 = 4\);
- Với \(x = 2 \Rightarrow f\left( 2 \right) = 2;g\left( 2 \right) = 2 + 3 = 5\);
Ta có bảng sau:
\(x\) | –2 | –1 | 0 | 1 | 2 |
\(y = f\left( x \right) = x\) | –2 | –1 | 0 | 1 | 2 |
\(y = g\left( x \right) = x + 3\) | 1 | 2 | 3 | 4 | 5 |
b)
- Vẽ đồ thị hàm số \(y = f\left( x \right) = x\)
Cho \(x = 1 \Rightarrow y = f\left( x \right) = 1\). Ta vẽ điểm \(A\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\).
- Các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) trong bảng trên là \(B\left( { - 2;1} \right);C\left( { - 1;2} \right);D\left( {0;3} \right);E\left( {1;4} \right);F\left( {2;5} \right)\).
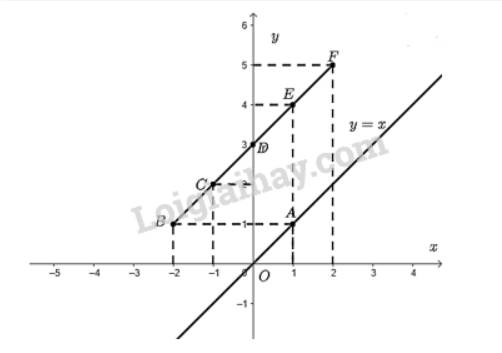
c) Ta đặt thước thẳng kiểm tra thì thấy các điểm thuộc đồ thị hàm số \(y = g\left( x \right) = x = 3\) thẳng hàng với nhau.
Dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\):
Bước 1: Chọn hai điểm \(A;B\) phân biệt thuộc đồ thị hàm số \(y = g\left( x \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A;B\).
Đồ thị hàm số \(y = g\left( x \right)\) là đường thẳng đi qua hai điểm \(A;B\).

a: 
b: Tọa độ A là:
\(\left\{{}\begin{matrix}3x+3=-2x+8\\y=-2x+8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=5\\y=-2x+8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=-2+8=6\end{matrix}\right.\)
Vậy: A(1;6)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\3x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+1=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\-2x+8=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-2x=-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)
Vậy: A(1;6); B(-1;0); C(4;0)
\(AB=\sqrt{\left(-1-1\right)^2+\left(0-6\right)^2}=2\sqrt{10}\)
\(AC=\sqrt{\left(4-1\right)^2+\left(0-6\right)^2}=3\sqrt{5}\)
\(BC=\sqrt{\left(4+1\right)^2+\left(0-0\right)^2}=5\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot BA\cdot AC}=\dfrac{40+45-25}{2\cdot2\sqrt{10}\cdot3\sqrt{5}}=\dfrac{\sqrt{2}}{2}\)
=>\(sinBAC=\sqrt{1-\left(\dfrac{\sqrt{2}}{2}\right)^2}=\dfrac{\sqrt{2}}{2}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\cdot2\sqrt{10}\cdot3\sqrt{5}=15\)

a:
b: Phương trình hoành độ giao điểm là:
3x=x-4
=>2x=-4
=>x=-2
Thay x=-2 vào y=x-4, ta được:
y=-2-4=-6
Vậy: Tọa độ giao điểm là A(-2;-6)