
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi độ dài mỗi cạnh của tam giác lần lượt là x;y;z
Theo bài ra ta có:
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\) và x+y+z=72
theo tính chất dãy tỉ số bằng nhau ta có
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{72}{12}=6\)
=> x=18
y=24
z=30
Bài 21:
Gọi độ dài 3 cạnh của tam giác đó là: a, b, c ( a, b, c > 0 )
Theo đề bài, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) và a + b + c = 72
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{72}{12}=6\)
Do đó:
\(\frac{a}{3}=6=>a=6\cdot3=18\)
\(\frac{b}{4}=6=>b=6\cdot4=24\)
\(\frac{c}{5}=6=>c=6\cdot5=30\)
Vậy độ dài 3 cạnh của tam giác đó theo thứ tự là: 18; 24; 30 ( cm ) thỏa mãn yêu cầu đề bài
Bài 22:
Gọi số học sinh 3 lớp 7A, 7B, 7C theo thứ tự là: a, b, c ( a, b, c thuộc N* )
Theo đề bài, ta có:
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}\) và c - a = 16
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{c-a}{6-4}=\frac{16}{2}=8\)
Do đó:
\(\frac{a}{4}=8=>a=8\cdot4=32\)
\(\frac{b}{5}=8=>b=8\cdot5=40\)
\(\frac{c}{6}=8=>c=8\cdot6=48\)
Vậy số học sinh 3 lớp 7A, 7B, 7C theo thứ tự là: 32; 40; 48 ( học sinh ) thỏa mãn yêu cầu đề bài

22:
a:
\(\overrightarrow{AD}=2\overrightarrow{DB}\)
=>\(\overrightarrow{AD}=\dfrac{2}{3}\overrightarrow{AB}\)
\(\overrightarrow{CE}=3\overrightarrow{EA}\)
=>\(\overrightarrow{AE}=\dfrac{1}{3}\overrightarrow{EC}\)
=>\(\overrightarrow{AE}=\dfrac{1}{4}\overrightarrow{AC}\)
Xét ΔAED có AM là trung tuyến
nên \(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{AE}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{8}\overrightarrow{AC}\)
b: \(\overrightarrow{MI}=\overrightarrow{ME}+\overrightarrow{EI}\)
\(=\dfrac{1}{2}\overrightarrow{DE}+\overrightarrow{EC}+\overrightarrow{CI}\)
\(=\dfrac{1}{2}\left(\overrightarrow{DA}+\overrightarrow{AE}\right)+\dfrac{3}{4}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CB}\)
\(=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\right)+\dfrac{3}{4}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{AB}\)
\(=\dfrac{-1}{3}\overrightarrow{AB}+\dfrac{1}{8}\overrightarrow{AC}+\dfrac{3}{4}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AB}\)
\(=\dfrac{1}{6}\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AC}\)

\(P=\left(sin^2x-1\right)tan^2x+\left(cos^2x-1\right)cot^2x\)
\(=-cos^2x.\dfrac{sin^2x}{cos^2x}+\left(-sin^2x\right)\dfrac{cos^2x}{sin^2x}\)
\(=-sin^2x-cos^2x\)
\(=-\left(sin^2x+cos^2x\right)\)
\(=-1\)


Bài 1:
a: Ư(12)={1;2;3;4;6;12}
Ư(-17)={1;-1;17;-17}
Ư(22)={1;2;11;22}
b: B(4)={0;4;8;...}
B(-5)={0;-5;-10;...}
Bài 2:
x-2 là ước của -11
nên \(x-2\in\left\{1;-1;11;-11\right\}\)
hay \(x\in\left\{3;1;13;-9\right\}\)
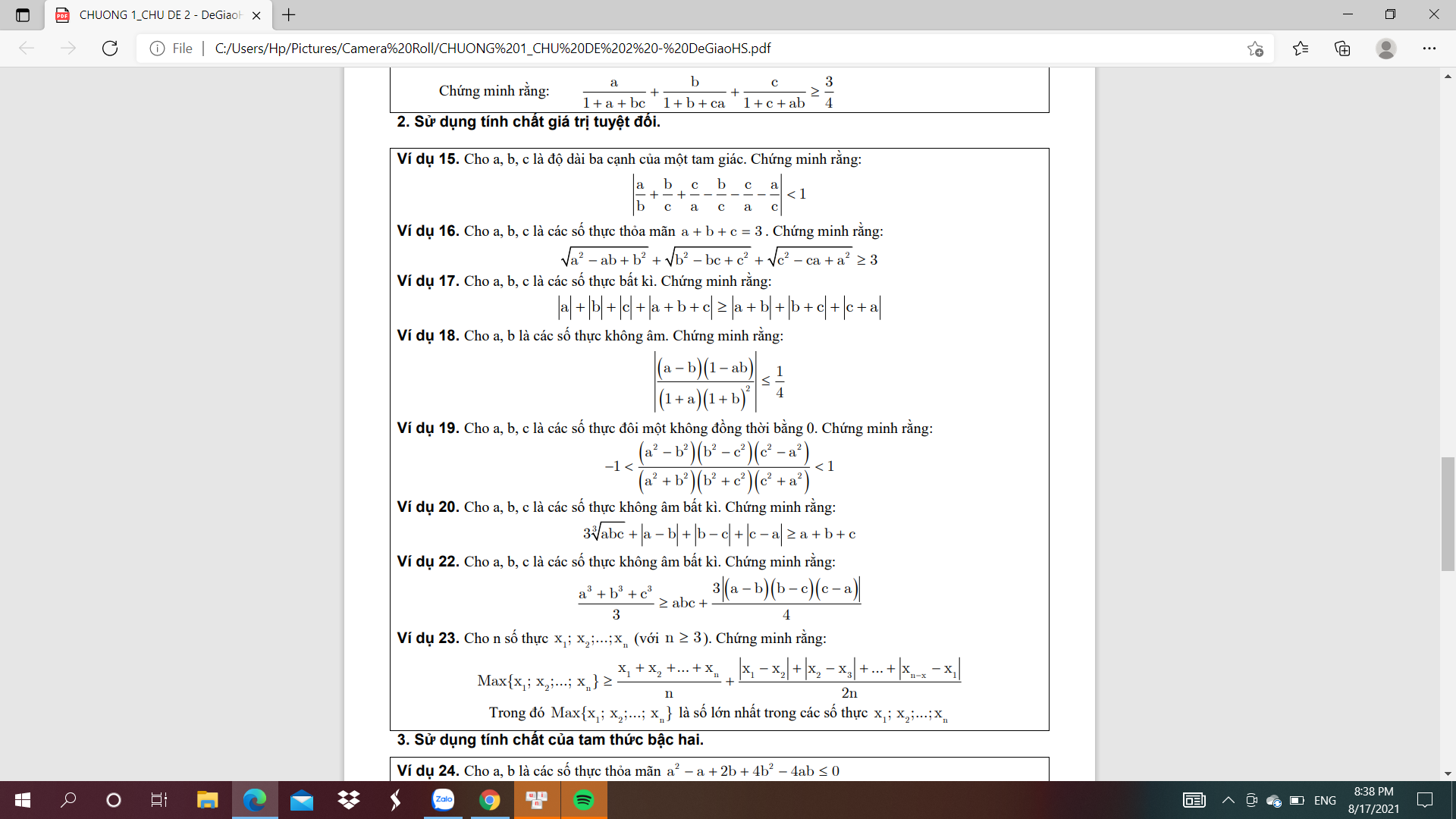
 và bài 22 giúp nhé
và bài 22 giúp nhé 
 giúp mình câu 22 với
giúp mình câu 22 với
 giúp e bài 17 với ạ? E ko biết cách làm như thế nào nên có thể hướng dẫn e ko ạ?
giúp e bài 17 với ạ? E ko biết cách làm như thế nào nên có thể hướng dẫn e ko ạ?
ai giúp với