Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\sqrt{8}-\sqrt{7}+5\sqrt{7}+2\sqrt{2}\\ =2\sqrt{2}-\sqrt{7}+5\sqrt{7}+2\sqrt{2}\\ =4\sqrt{2}+4\sqrt{7}\)
\(B=\left(3+2\sqrt{6}+2\right)\left(25-20\sqrt{6}+24\right)\sqrt{3-2\sqrt{6}+2}\\ =\left(\sqrt{3}+\sqrt{2}\right)^2\left(5-2\sqrt{6}\right)^2\left(\sqrt{3}-\sqrt{2}\right)\\ =\left(\sqrt{3}+\sqrt{2}\right)\left(3-2\sqrt{6}+2\right)^2\\ =\left(\sqrt{3}-\sqrt{2}\right)^3\\ =9\sqrt{3}-11\sqrt{2}\)

\(a.\sqrt{\left(1-\sqrt{5}\right)^2}+1=\left|1-\sqrt{5}\right|+1=\sqrt{5}-1+1=\sqrt{5}\)
\(b.\sqrt{3+2\sqrt{2}}-2=\sqrt{\left(\sqrt{2}+1\right)^2}-2=\sqrt{2}+1-2=\sqrt{2}-1\)
\(c.\sqrt{b^2-b+\dfrac{1}{4}}-\left(2b-\dfrac{1}{2}\right)=\sqrt{\left(b-\dfrac{1}{2}\right)^2}-2b+\dfrac{1}{2}=b-\dfrac{1}{2}-2b+\dfrac{1}{2}=-2b\)
\(d.\sqrt{7+2\sqrt{10}}=\sqrt{\left(\sqrt{5}+\sqrt{2}\right)^2}=\sqrt{5}+\sqrt{2}\)
\(e.\sqrt{11-4\sqrt{7}}=\sqrt{\left(\sqrt{7}-2\right)^2}=\sqrt{7}-2\)
\(g.3x+\sqrt{x^2-2x+1}=3x+\sqrt{\left(x-1\right)^2}\)
* \(x\ge1\Rightarrow3x+\left|x-1\right|=3x+x-1=4x-1\)
* \(x< 1\Rightarrow3x+\left|x-1\right|=3x+1-x=2x+1\)
\(h.\sqrt{y+2\sqrt{y^2-2y+1}}=\sqrt{y+2\sqrt{\left(y-1\right)^2}}=\sqrt{y+2y-2}=\sqrt{3y-2}\left(y\ge1\right)\) hoặc: \(\sqrt{y+2-2y}=\sqrt{-y+2}\left(y< 1\right)\)
\(H=\sqrt{17-2\sqrt{32}}+\sqrt{17+2\sqrt{32}}\)
\(H^2=17-2\sqrt{32}+17+2\sqrt{32}+2\sqrt{\left(17-2\sqrt{32}\right)\left(17+2\sqrt{32}\right)}=34+2\sqrt{161}\)
\(H=\sqrt{34+2\sqrt{161}}\)
\(k.\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}=\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}=2\sqrt{2}\)

a: \(A=\dfrac{\sqrt{2}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}-\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{2}-\sqrt{2}=0\)
b: \(B=\left(1+\sqrt{2}\right)\left(1-\sqrt{2}\right)=1-2=-1\)
c: \(B=\left(\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{-\left(\sqrt{3}-1\right)}\right)\cdot\left(\sqrt{3}-\sqrt{2}\right)\)
\(=-\sqrt{2}\left(\sqrt{3}-\sqrt{2}\right)\)
\(=-\sqrt{6}+2\)


Câu 1:
Có: \(8-4\sqrt{3}=8-2\sqrt{12}=6+2-2\sqrt{6.2}=(\sqrt{6}-\sqrt{2})^2\)
\(\Rightarrow \sqrt{8-4\sqrt{3}}=\sqrt{6}-\sqrt{2}\)
Do đó:
\(\frac{\sqrt{8-4\sqrt{3}}}{\sqrt{\sqrt{6}-\sqrt{2}}}.\sqrt{\sqrt{6}+\sqrt{2}}=\frac{\sqrt{6}-\sqrt{2}}{\sqrt{\sqrt{6}-\sqrt{2}}}.\sqrt{\sqrt{6}+\sqrt{2}}=\sqrt{\sqrt{6}-\sqrt{2}}.\sqrt{\sqrt{6}+\sqrt{2}}\)
\(=\sqrt{(\sqrt{6})^2-(\sqrt{2})^2}=\sqrt{6-2}=2\)
Câu 2:
\(16-5\sqrt{7}=\frac{32-10\sqrt{7}}{2}=\frac{32-2\sqrt{175}}{2}=\frac{25+7-2\sqrt{25.7}}{2}=\frac{(5-\sqrt{7})^2}{2}\)
\(\Rightarrow \sqrt{16-5\sqrt{7}}=\frac{5-\sqrt{7}}{\sqrt{2}}\)
Do đó:
\(\sqrt{16-5\sqrt{7}}(5\sqrt{2}+\sqrt{14})+\frac{6}{3+\sqrt{10}}=\frac{5-\sqrt{7}}{\sqrt{2}}.\sqrt{2}(5+\sqrt{7})+\frac{6(3-\sqrt{10})}{(3+\sqrt{10})(3-\sqrt{10})}\)
\(=(5-\sqrt{7})(5+\sqrt{7})+\frac{18-6\sqrt{10}}{3^2-10}=25-7+(-18+6\sqrt{10})\)
\(=6\sqrt{10}\)

1: \(=\sqrt{6}+\sqrt{6}+1=2\sqrt{6}+1\)
2: \(=\dfrac{6\left(1-\sqrt{3}\right)}{1-\sqrt{3}}+\dfrac{3\left(\sqrt{3}+1\right)}{\sqrt{3}+1}=6+3=9\)
3: \(=\sqrt{3}+1-\sqrt{3}=1\)

a: \(=\left(-\sqrt{5}-\sqrt{7}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)\)
\(=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
=-2
b: \(=\sqrt{2-\sqrt{3}}+\sqrt{2+\sqrt{3}}\)
\(=\dfrac{\sqrt{4-2\sqrt{3}}+\sqrt{4+2\sqrt{3}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{3}-1+\sqrt{3}+1}{\sqrt{2}}=\sqrt{6}\)
c: \(=\dfrac{\sqrt{10}\left(\sqrt{2}-\sqrt{5}\right)}{\sqrt{2}-\sqrt{5}}-2-\sqrt{10}+3\sqrt{7}+2\)
\(=\sqrt{10}-\sqrt{10}+3\sqrt{7}=3\sqrt{7}\)

Bài 1:
a. Ta có \(\sqrt{\dfrac{2}{x^2}}=\dfrac{\sqrt{2}}{\left|x\right|}=\dfrac{\sqrt{2}}{x}\) ,để biểu thức có nghĩa thì \(x>0\)
b. Để biểu thức \(\sqrt{\dfrac{-3}{3x+5}}\) có nghĩa thì \(\dfrac{-3}{3x+5}\ge0\)
mà \(-3< 0\Rightarrow3x+5< 0\) \(\Rightarrow x< \dfrac{-5}{3}\)
Bài 2:
a. \(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}=\dfrac{\left(2+\sqrt{2}\right)\left(1-\sqrt{2}\right)}{1-2}=\dfrac{-\sqrt{2}}{-1}=\sqrt{2}\)
b. \(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right)\sqrt{7}+7\sqrt{8}\)
\(=14-14\sqrt{2}+7+14\sqrt{2}\)
\(=21\)
c. \(\left(\sqrt{14}-3\sqrt{2}\right)^2+6\sqrt{28}\)
\(=14-6\sqrt{28}+18+6\sqrt{28}\)
\(=32\)
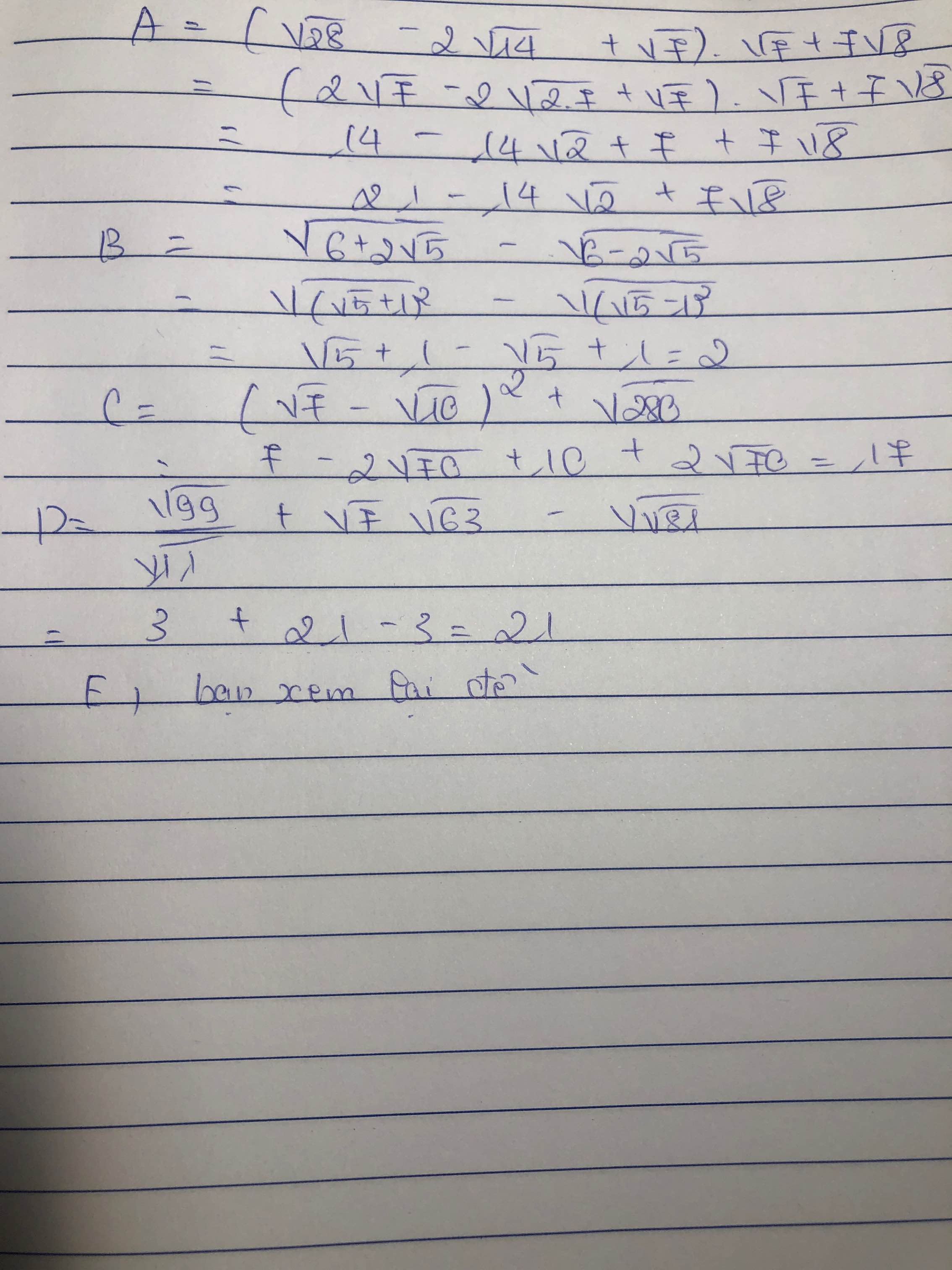
Bài 1:
a: \(=\sqrt{32.4}=\dfrac{9}{5}\sqrt{10}\)
b: \(=\sqrt{5\cdot5\cdot7\cdot7\cdot11\cdot11}=5\cdot7\cdot11=385\)
c: \(=5-2\sqrt{6}\)
d: \(=18-1=17\)
e: \(=3\sqrt{2}-2\sqrt{3}+7\sqrt{3}-7\sqrt{2}=-4\sqrt{2}+5\sqrt{3}\)