Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{2}{5}\)
b) Ta có: \(9x^2-6x+2\)
\(=9x^2-6x+1+1\)
\(=\left(3x-1\right)^2+1\ge1\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{3}\)
c) Ta có: \(-x^2+2x-2\)
\(=-\left(x^2-2x+2\right)\)
\(=-\left(x^2-2x+1+1\right)\)
\(=-\left(x-1\right)^2-1\le-1\forall x\)
Dấu '=' xảy ra khi x-1=0
hay x=1
d) Ta có: \(x^2+12x+39\)
\(=x^2+12x+36+3\)
\(=\left(x+6\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi x=-6
e) Ta có: \(-x^2-12x\)
\(=-\left(x^2+12x+36-36\right)\)
\(=-\left(x+6\right)^2+36\le36\forall x\)
Dấu '=' xảy ra khi x=-6
f) Ta có: \(4x-x^2+1\)
\(=-\left(x^2-4x-1\right)\)
\(=-\left(x^2-4x+4-5\right)\)
\(=-\left(x-2\right)^2+5\le5\forall x\)
Dấu '=' xảy ra khi x=2

a) Ta có: \(25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{2}{5}\)
b) Ta có: \(9x^2-6x+2\)
\(=9x^2-6x+1+1\)
\(=\left(3x-1\right)^2+1\ge1\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{3}\)
c) Ta có: \(-x^2+2x-2\)
\(=-\left(x^2-2x+2\right)\)
\(=-\left(x^2-2x+1+1\right)\)
\(=-\left(x-1\right)^2-1\le-1\forall x\)
Dấu '=' xảy ra khi x=1
( Mình trình bày mẫu câu a các câu khác mình làm tắt lại nhưng tương tự trình bày câu a nha )
a, Ta có : \(25x^2-20x+7=\left(5x\right)^2-2.5x.2+2^2+3\)
\(=\left(5x-2\right)^2+3\)
Thấy : \(\left(5x-2\right)^2\ge0\forall x\in R\)
\(\Rightarrow\left(5x-2\right)^2+3\ge3\forall x\in R\)
Vậy \(Min=3\Leftrightarrow5x-2=0\Leftrightarrow x=\dfrac{2}{5}\)
b, \(=9x^2-2.3x+1+1=\left(3x-1\right)^2+1\ge1\)
Vậy Min = 1 <=> x = 1/3
c, \(=-x^2+2x-1-1=-\left(x^2-2x+1\right)-1=-\left(x-1\right)^2-1\le-1\)
Vậy Max = -1 <=> x = 1
d, \(=x^2+2.x.6+36+3=\left(x+6\right)^2+3\ge3\)
Vậy Min = 3 <=> x = - 6
e, \(=-x^2-2.x.6-36+36=-\left(x+6\right)^2+36\le36\)
Vậy Max = 36 <=> x = -6 .
f, \(=-x^2+4x-4+5=-\left(x^2-4x+4\right)+5=-\left(x-2\right)^2+5\le5\)
Vậy Max = 5 <=> x = 2

a: A=(x-1)(x-3)(x2-4x+5)
\(=\left(x^2-4x+3\right)\left(x^2-4x+5\right)\)
\(=\left(x^2-4x\right)^2+8\left(x^2-4x\right)+15\)
\(=\left(x^2-4x+4\right)^2-1\)
\(=\left(x-2\right)^4-1>=-1\)
Dấu = xảy ra khi x-2=0
=>x=2
b: \(B=x^2-2xy+2y^2-2y+1\)
\(=x^2-2xy+y^2+y^2-2y+1\)
\(=\left(x-y\right)^2+\left(y-1\right)^2>=0\)
Dấu = xảy ra khi x-y=0 và y-1=0
=>x=y=1
c: \(C=5+\left(1-x\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)
\(=-\left(x-1\right)\left(x+6\right)\left(x+2\right)\left(x+3\right)+5\)
\(=-\left(x^2+5x-6\right)\left(x^2+5x+6\right)+5\)
\(=-\left[\left(x^2+5x\right)^2-36\right]+5\)
\(=-\left(x^2+5x\right)^2+36+5\)
\(=-\left(x^2+5x\right)^2+41< =41\)
Dấu = xảy ra khi \(x^2+5x=0\)
=>x(x+5)=0
=>\(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)

\(A=-x^2+2xy-4y^2+2x+10y-3\)
\(=-x^2+2xy-y^2+2x-2y-1-3y^2+12y-12+10\)
\(=-\left(x^2-2xy+y^2-2x+2y+1\right)-3\left(y^2-4y+4\right)+10\)
\(=-\left(x-y-1\right)^2-3\left(y-2\right)^2+10< =10\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-y-1=0\\y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=y+1=3\end{matrix}\right.\)
\(B=-4x^2-5y^2+8xy+10y+12\)
\(=-4x^2+8xy-4y^2-y^2+10y-25+37\)
\(=-4\left(x^2-2xy+y^2\right)-\left(y^2-10y+25\right)+37\)
\(=-4\left(x-y\right)^2-\left(y-5\right)^2+37< =37\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-y=0\\y-5=0\end{matrix}\right.\)
=>x=y=5

/x-3/>=0\(\Rightarrow\)-/x-3/<=0 maxP=12 khi x-3=0 \(\Rightarrow\)x=3
\(P=-\left|x-3\right|+12\)
Vì \(-\left|x-3\right|\le0\Leftrightarrow-\left|x-3\right|+12\le12\)
Vậy GTLN của P là 12 tại \(-\left|x-3\right|=0\Leftrightarrow x=0\)
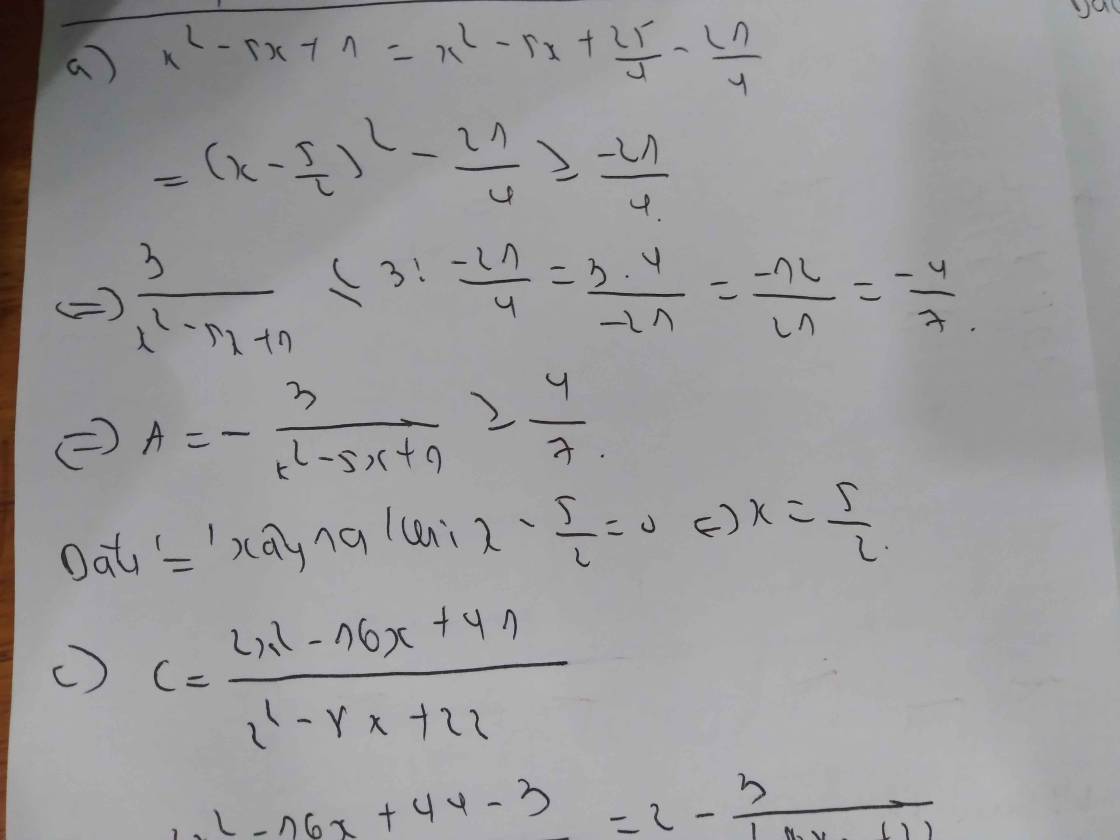
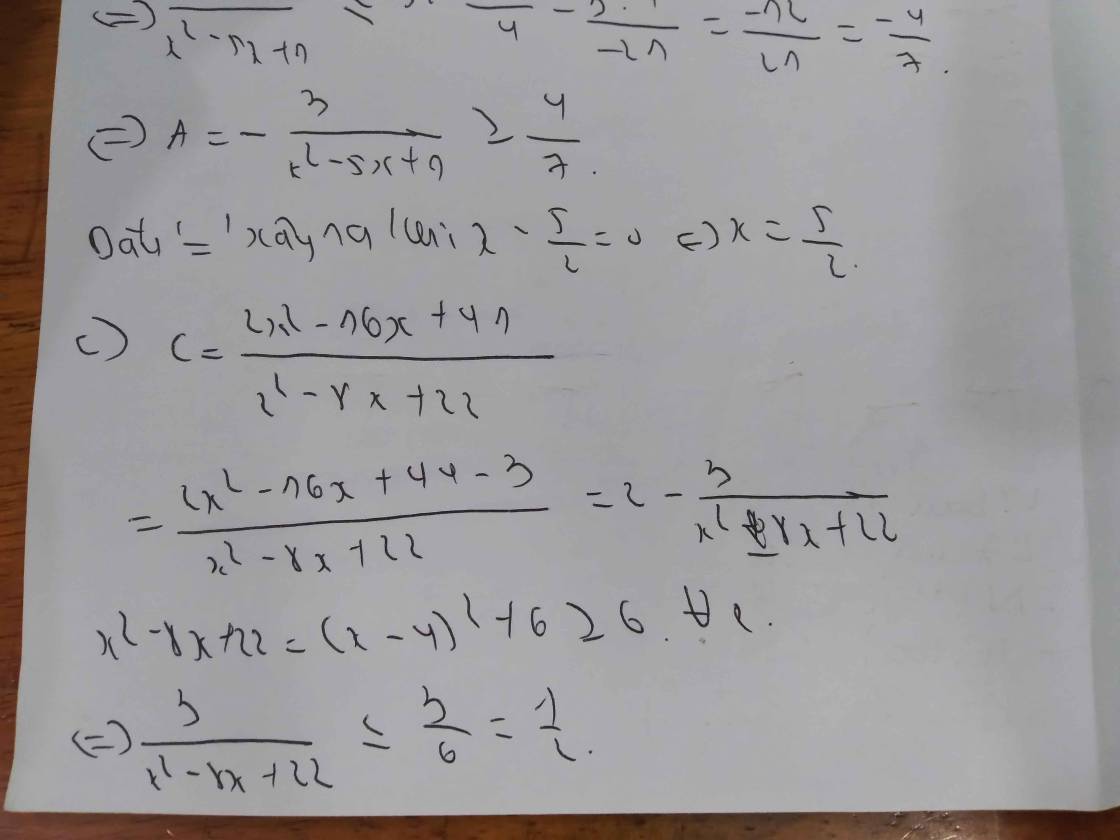
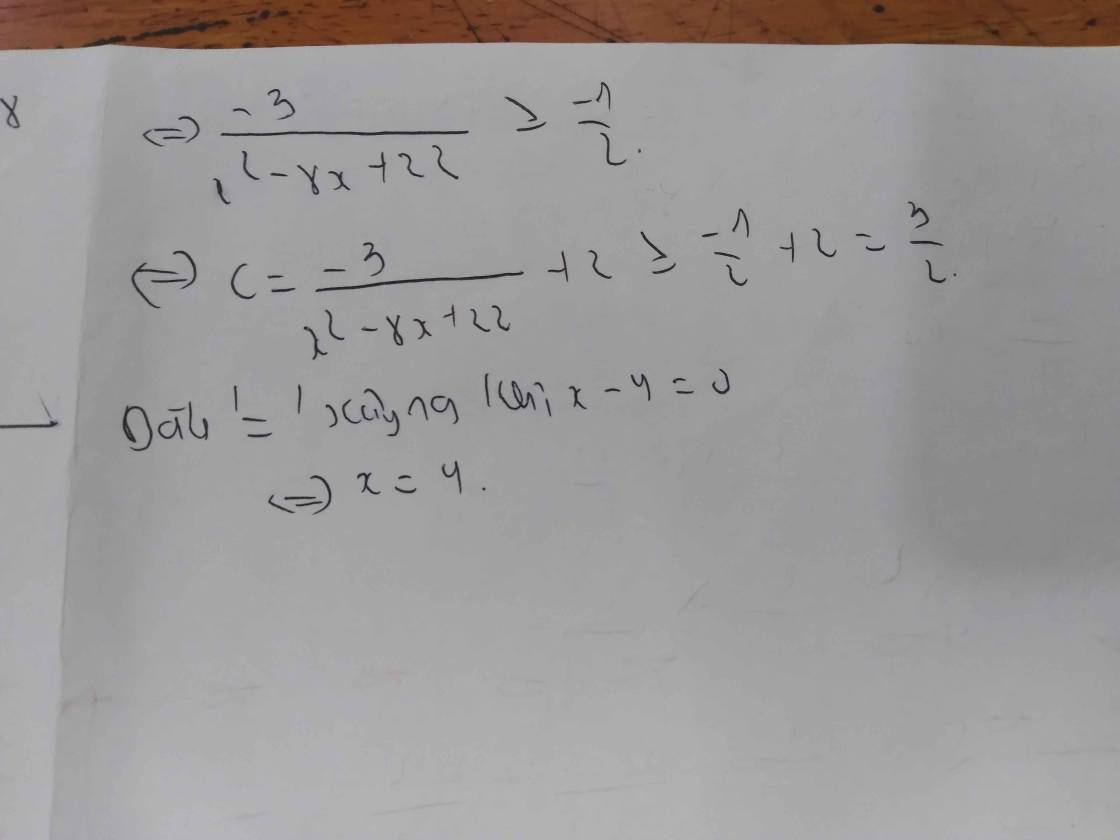

\(A=\left|4x-3\right|+\left|5y+7,5\right|+17,5\)
|4x - 3| lớn hơn hoặc bằng 0
|5y + 7,5| lớn hơn hoặc bằng 0
|4x - 3| + |5y + 7,5| +17,5 lớn hơn hoặc bằng 17,5
Vậy Max A = 17,5 khi x = \(\frac{3}{4}\) và y = \(-1,5\)
sorry, i cant do it