K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 6 2021
`A=(10^14-1)/(10^15-11)`
`=>10A=(10^15-10)/(10^15-11)`
`=>10A=(10^15-11+1)/(10^15-11)`
`=>10A=1+1/(10^15-1)`
`=>A>1/10`
`B=(10^14+1)/(10^15+9)`
`=>10B=(10^15+10)/(10^15+9)`
`=>10A=(10^15+9+1)/(10^15+9)`
`=>10A=1+1/(10^15+9)`
Vì `1/(10^15-1)>1/(10^15+9)`
`=>10B>10A`
`=>B>A`
13 tháng 6 2021
Giải:
\(A=\dfrac{10^{14}-1}{10^{15}-11}\)
\(10A=\dfrac{10^{15}-10}{10^{15}-11}\)
\(10A=\dfrac{10^{15}-11+1}{10^{15}-11}\)
\(10A=1+\dfrac{1}{10^{15}-11}\)
Tương tự:
\(B=\dfrac{10^{14}+1}{10^{15}+9}\)
\(10B=\dfrac{10^{15}+10}{10^{15}+9}\)
\(10B=\dfrac{10^{15}+9+1}{10^{15}+9}\)
\(10B=1+\dfrac{1}{10^{15}+9}\)
Vì \(\dfrac{1}{10^{15}-11}>\dfrac{1}{10^{15}+9}\) nên \(10A>10B\)
\(\Rightarrow A>B\)
Chúc bạn học tốt!
2N
1
9 tháng 2 2022
a)
\(\dfrac{-2}{3}\)>\(\dfrac{5}{-8}\)
b)
\(\dfrac{398}{-412}\)<\(\dfrac{-25}{-137}\)
c)
\(\dfrac{-14}{21}\)<\(\dfrac{60}{72}\)
2N
2
PT
1
CM
26 tháng 9 2019
10 A = 10 16 + 10 10 16 + 1 = 1 + 9 10 16 + 1 10 B = 10 17 + 10 10 17 + 1 = 1 + 9 10 17 + 1
Vì 9 10 16 + 1 > 9 10 17 + 1 nên 10 A > 10 B
Vậy A > B
QH
1
KV
15 tháng 8 2023
a) \(5^{48}=\left(5^4\right)^{12}=625^{12}\)
\(2^{108}=\left(2^9\right)^{12}=512^{12}\)
Do \(625>512\Rightarrow625^{12}>512^{12}\) \(\Rightarrow5^{48}>2^{108}\) (1)
Lại có: \(108>105\Rightarrow2^{108}>2^{105}\) (2)
Từ (1) và (2) \(\Rightarrow5^{48}>2^{105}\)
b) \(2^{50}=\left(2^5\right)^{10}=32^{10}\)
Do \(33>32\Rightarrow33^{10}>32^{10}\)
Vậy \(33^{10}>2^{50}\)
c) Do \(513>512\Rightarrow513^{100}>512^{100}\) (1)
\(512^{100}=\left(2^9\right)^{100}=2^{900}\) \(=2^{10.90}=\left(2^{10}\right)^{90}=1024^{90}\) (2)
Do \(1024>1023\Rightarrow1024^{90}>1023^{90}\) (3)
Từ (1), (2) và (3) \(\Rightarrow513^{100}>1023^{90}\)
DN
1
4 tháng 7 2021
Giải:
a) Gọi dãy đó là A, ta có:
\(A=\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2014}}\)
\(2A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2013}}\)
\(2A-A=\left(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2013}}\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2014}}\right)\)
\(A=\dfrac{1}{2}-\dfrac{1}{2^{2014}}\)
Vì \(\dfrac{1}{2}< 1;\dfrac{1}{2^{2014}}< 1\) nên \(\dfrac{1}{2}-\dfrac{1}{2^{2014}}< 1\)
\(\Rightarrow A< 1\)
b) \(A=\dfrac{10^{11}-1}{10^{12}-1}\) và \(B=\dfrac{10^{10}+1}{10^{11}+1}\)
Ta có:
\(A=\dfrac{10^{11}-1}{10^{12}-1}\)
\(10A=\dfrac{10^{12}-10}{10^{12}-1}\)
\(10A=\dfrac{10^{12}-1+9}{10^{12}-1}\)
\(10A=1+\dfrac{9}{10^{12}-1}\)
Tương tự:
\(B=\dfrac{10^{10}+1}{10^{11}+1}\)
\(10B=\dfrac{10^{11}+10}{10^{11}+1}\)
\(10B=\dfrac{10^{11}+1+9}{10^{11}+1}\)
\(10B=1+\dfrac{9}{10^{11}+1}\)
Vì \(\dfrac{9}{10^{12}-1}< \dfrac{9}{10^{11}+1}\) nên \(10A< 10B\)
\(\Rightarrow A< B\)
XN
3
26 tháng 9 2021
b)
a = 25.26 261 = 25.(26 260 +1) = 25.10.2626 + 25 = 25.10.26.101 + 25
b = 26.25 251 = 26.(25 250 + 1) = 26.10.2525 + 26 = 26.10.25.101 + 26
Suy ra a < b
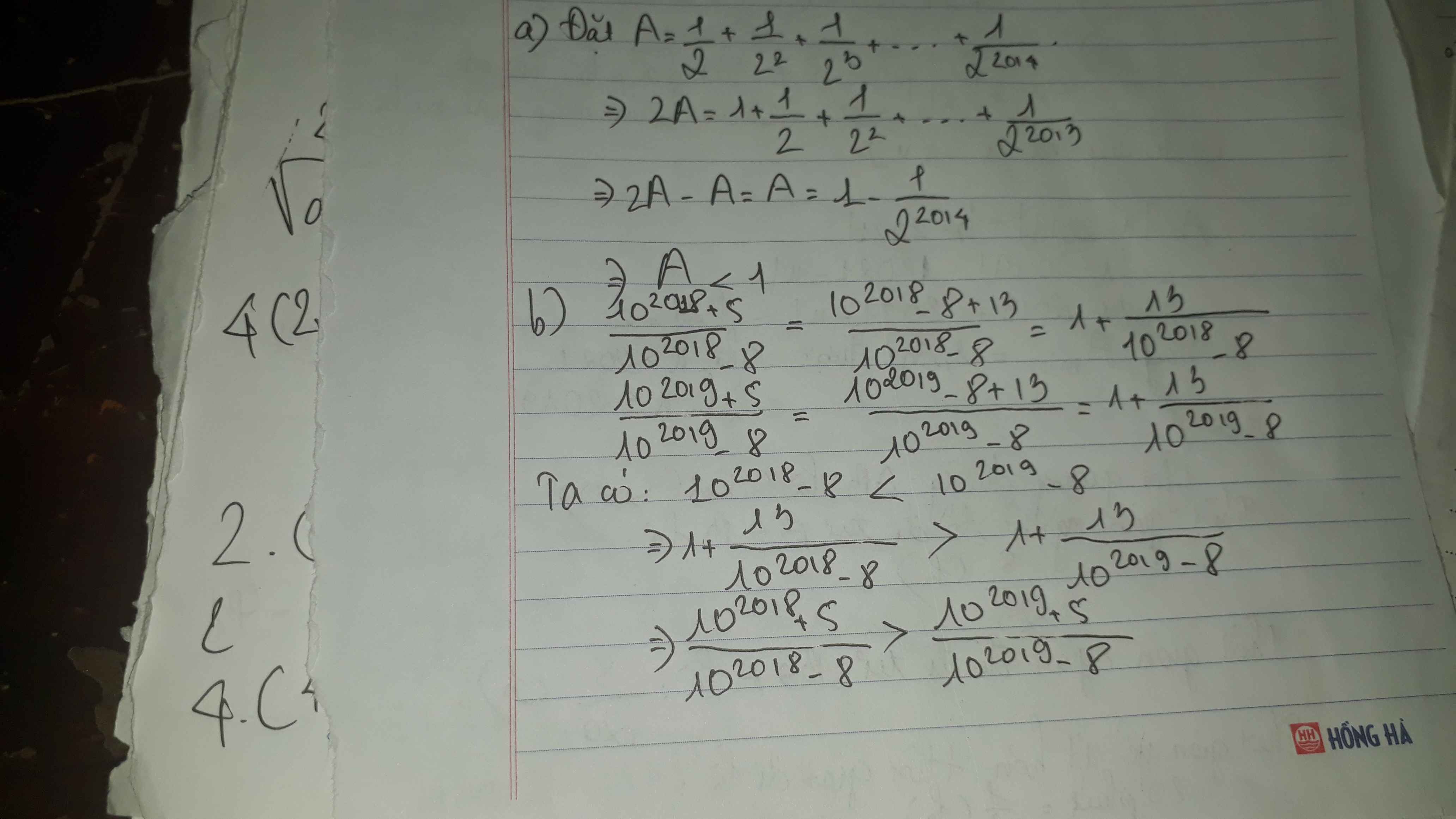
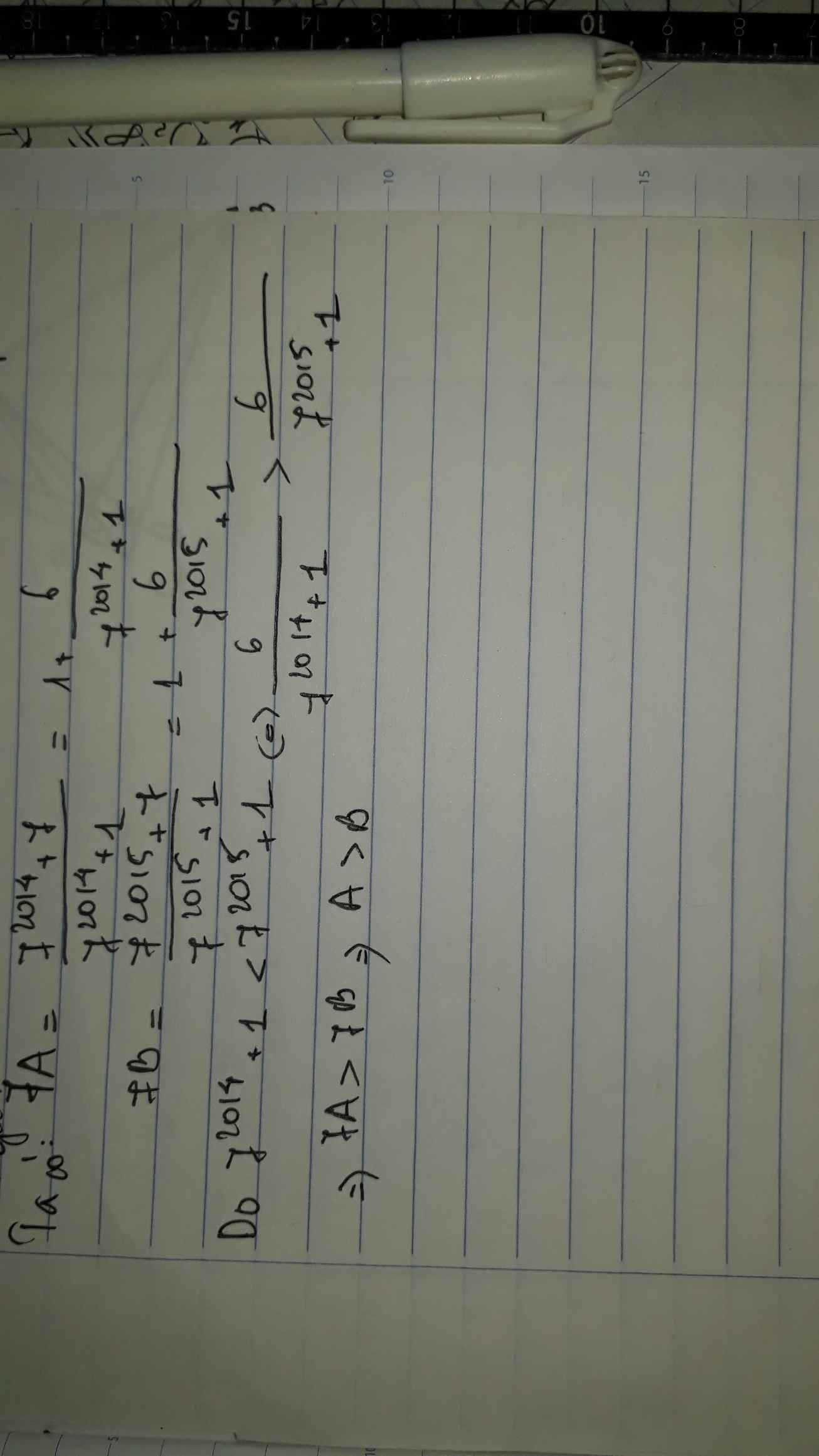
\(a.4^8< 3.8^5\)
\(b.10^{15}>26^3\)
a) 48 < 3.85
b) 1015 > 263