
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{1313}{1717}=\dfrac{101x13}{101x17}=\dfrac{13}{17}\)
\(\dfrac{131313}{171717}=\dfrac{10101x13}{10101x17}=\dfrac{13}{17}\)
Vậy \(\dfrac{1313}{1717}=\dfrac{131317}{171717}\)
\(\dfrac{1313}{1717}và\dfrac{131313}{171717}\\ \dfrac{1313}{1717}=\dfrac{13}{17}\\ \dfrac{131313}{171717}=\dfrac{13}{17}\\ \Rightarrow\dfrac{1313}{1717}=\dfrac{131313}{171717}\)

a) có 12/48 < 13/48, 13/48 < 13/47
=> 12/48 < 13/47
b) có 415/395 > 1 , 572/581 <1
=> 415/395 > 572/581

+ \(\frac{2000}{2001}=\frac{2001-1}{2001}=1-\frac{1}{2001}\)
+ \(\frac{2001}{2002}=\frac{2002-1}{2002}=1-\frac{1}{2002}\)
+ \(\frac{1}{2001}>\frac{1}{2002}\Rightarrow1-\frac{1}{2001}
\(1-\frac{2000}{2001}=\frac{1}{2001}\)
\(1-\frac{2001}{2002}=\frac{1}{2002}\)
Vì \(\frac{1}{2001}>\frac{1}{2002}\) nên \(\frac{2000}{2001}

Ta có: 2000/2001 = 1 - 1/2001
2001/2002 = 1 - 1/2002
mà 1/2001 > 1/2002
--> 1 - 1/2001 < 1 - 1/2002
--> 2000/2001 < 2001/2002

Vì\(\frac{7}{15}>\frac{7}{29};\frac{7}{29}>\frac{15}{29}\)
=>\(\frac{7}{15}>\frac{15}{29}\)
\(\frac{7}{15}< \frac{15}{29}\)
Chúc em hok tốt

ta có: \(\dfrac{2021}{2022}< 1\)
\(\dfrac{5}{4}>1\)
\(\Rightarrow\dfrac{2021}{2022}< 1< \dfrac{5}{4}\)
vậy \(\dfrac{2021}{2022}< \dfrac{5}{4}\)
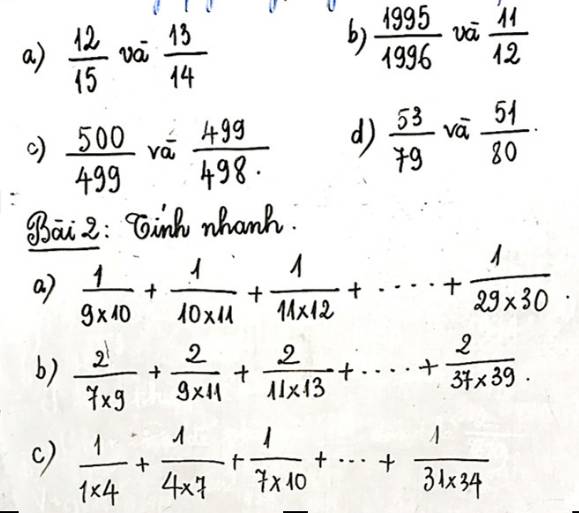
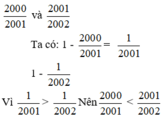
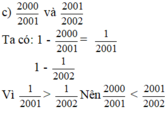
Bài 1 :
a) \(\dfrac{12}{15}< \dfrac{12}{14}< \dfrac{13}{14}\Rightarrow\dfrac{12}{15}< \dfrac{13}{14}\)
b) \(\dfrac{11}{12}< \dfrac{11+1984}{12+1984}=\dfrac{1995}{1996}\)
\(\Rightarrow\dfrac{11}{12}< \dfrac{1995}{1996}\)
c) \(\dfrac{499}{498}>\dfrac{499+1}{498+1}=\dfrac{500}{499}\)
\(\Rightarrow\dfrac{499}{498}>\dfrac{500}{499}\)
d) \(\dfrac{51}{80}< \dfrac{51}{79}< \dfrac{53}{79}\)
\(\Rightarrow\dfrac{51}{80}< \dfrac{53}{79}\)
Bài 2:
a) \(\dfrac{1}{9\times10}+\dfrac{1}{10\times11}+\dfrac{1}{11\times12}+...+\dfrac{1}{29\times30}\)
\(=\dfrac{1}{9}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{11}+...+\dfrac{1}{29}-\dfrac{1}{30}\)
\(=\dfrac{1}{9}-\dfrac{1}{30}\)
\(=\dfrac{10}{90}-\dfrac{3}{90}\)
\(=\dfrac{7}{90}\)
b) \(\dfrac{2}{7\times9}+\dfrac{2}{9\times11}+\dfrac{2}{11\times13}+....+\dfrac{2}{37\times39}\)
\(=\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+...+\dfrac{1}{37}-\dfrac{1}{39}\)
\(=\dfrac{1}{7}-\dfrac{1}{39}\)
\(=\dfrac{32}{273}\)
c) \(\dfrac{1}{1\times4}+\dfrac{1}{4\times7}+...+\dfrac{1}{31\times34}\)
\(=\dfrac{1}{3}\cdot\left[3\cdot\left(\dfrac{1}{1\times4}+\dfrac{1}{4\times7}+...+\dfrac{1}{31\times34}\right)\right]\)
\(=\dfrac{1}{3}\cdot\left(\dfrac{3}{1\times4}+\dfrac{3}{4\times7}+...+\dfrac{3}{31\times34}\right)\)
\(=\dfrac{1}{3}\cdot\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{31}-\dfrac{1}{34}\right)\)
\(=\dfrac{1}{3}\cdot\left(1-\dfrac{1}{34}\right)\)
\(=\dfrac{1}{3}\cdot\dfrac{33}{34}\)
\(=\dfrac{11}{34}\)