Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét tứ giác AHCE có
IA=IC (đề bài)
IH=IE (đề bài)
=> AHCE là hbh (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
^AHC=90 (AH vuông góc BC)
=> AHCE là HCN
b/
+ Xét tg AHC có
IA=IC => HI là trung tuyến
MH=MC (đề bài) => AM là trung tuyến
=> G là trọng tâm của tam giác AHC \(\Rightarrow IG=\frac{IH}{3}\Rightarrow IG=\frac{GH}{2}\)
+ Xét tam giác ACE chứng minh tương tự ta cũng có \(IK=\frac{IE}{3}\Rightarrow IK=\frac{KE}{2}\)
Mà IH = IE
=> IK=IG => GH=KE=KI+KG=GK

a: Xét tứ giác AHCE có
I là trung điểm của AC
I là trung điểm của HE
Do đó: AHCE là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật
b: Xét ΔHKC có
M là trung điểm của HC
MG//KC
Do đó:G là trung điểm của HK
=>HG=GK(1)
Xét ΔEGC có
N là trung điểm của EC
NK//GC
Do đó: K là trung điểm của EG
=>EK=KG(2)
Từ (1) và (2) suy ra EK=KG=HG

A B C H E I M N G K
a/
Ta có
IA=IC (gt)
IH=IE (gt)
=> AHCE là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
\(AH\perp BC\Rightarrow\widehat{AHC}=90^o\)
=> AHCE là hình chữ nhật (hình bình hành có 1 góc vuông là HCN)
b/
Xét tg AHC có
MH=MC (gt)
IA=IC (gt)
=> G là trong tâm của tg AHC \(\Rightarrow HG=2IG\) (1)
\(\Rightarrow HG+IG=IH=3IG\) (2)
Chứng minh tương tự ta có K là trọng tâm của tg ACE
\(\Rightarrow KE=2IK\left(3\right)\Rightarrow KE+IK=IE=3IK\) (4)
Mà IH=IE (gt) (5)
Từ (2) (4) (5) => IG=IK (6)
Từ (1) (3) (6) => HG=KE
Mà IG=IK => IG+IKGK=2IK=KE
=> HG=GK=KE

xét tam giác ahc có hi và am là trung tuyến của tam giác nên k là trọng tâm tam giác ahc.
suy ra ik=1/3IH => ik=1/2kh.
chứng minh tương tự ta có ig=1/2ge.
Ta có IH=IE nên ik=ig => hk=ge=2ik
Mà 2ik=kg nên HG=GK=KE

mn ơi đừng hỉu lầm tên em nha tên thật của em là minDi còn tên trân là tên cháu em lớp 4

Bạn tự vẽ hình nhé.
a) Theo bài ra ta có:
Hai đường AC và HE cắt nhau tại trung điểm của mỗi đường
\(\Rightarrow\)AECH là hình bình hành
Lại có AH vuông góc với BC nên \(\widehat{AHC}=90^0\)
\(\Rightarrow\)AHCE là hình chữ nhật.
b) Xét tam giác AHC có:
AM và HI là hai đường trung tuyến của tam giác AHC
Mà hai đường này giao nhau tại G \(\Rightarrow\)G là trọng tâm của tam giác AHC
\(\Rightarrow GI=\frac{1}{3}HI\)và \(GI=\frac{1}{2}HG\)
Xét tam giác AEC có:
EI và AN là hai đường trung tuyến của tam giác AEC
Mà hai đường này giao nhau tại K \(\Rightarrow\)K là trọng tâm của tam giác AEC
\(\Rightarrow KI=\frac{1}{3}EI\)và \(KI=\frac{1}{2}KE\)
Mà IH = IE theo giả thiết nên IG = IK
\(\Rightarrow2IG=2IK=HG=KE=IG+IK=GK\)
\(\Rightarrow HG=GK=KE\left(ĐPCM\right)\)

a: Xét tứ giác AHCE có
I là trung điểm chung của AC và HE
góc AHC=90 độ
=>AHCE là hình chữ nhật
b: Xét ΔAHC có
HI,AM là trung tuyến
HI cắt AM tại G
=>G là trọng tâm
=>HG=2/3HI=2/3*1/2*HE=1/3HE
Xét ΔCAE có
AN,EI là trung tuyến
AN cắt EI tại K
=>K là trọng tâm
=>EK=2/3EI=1/3EH
HG+GK+KE=HE
=>GK=HE-1/3HE-1/3HE=1/3HE
=>HG=GK=KE
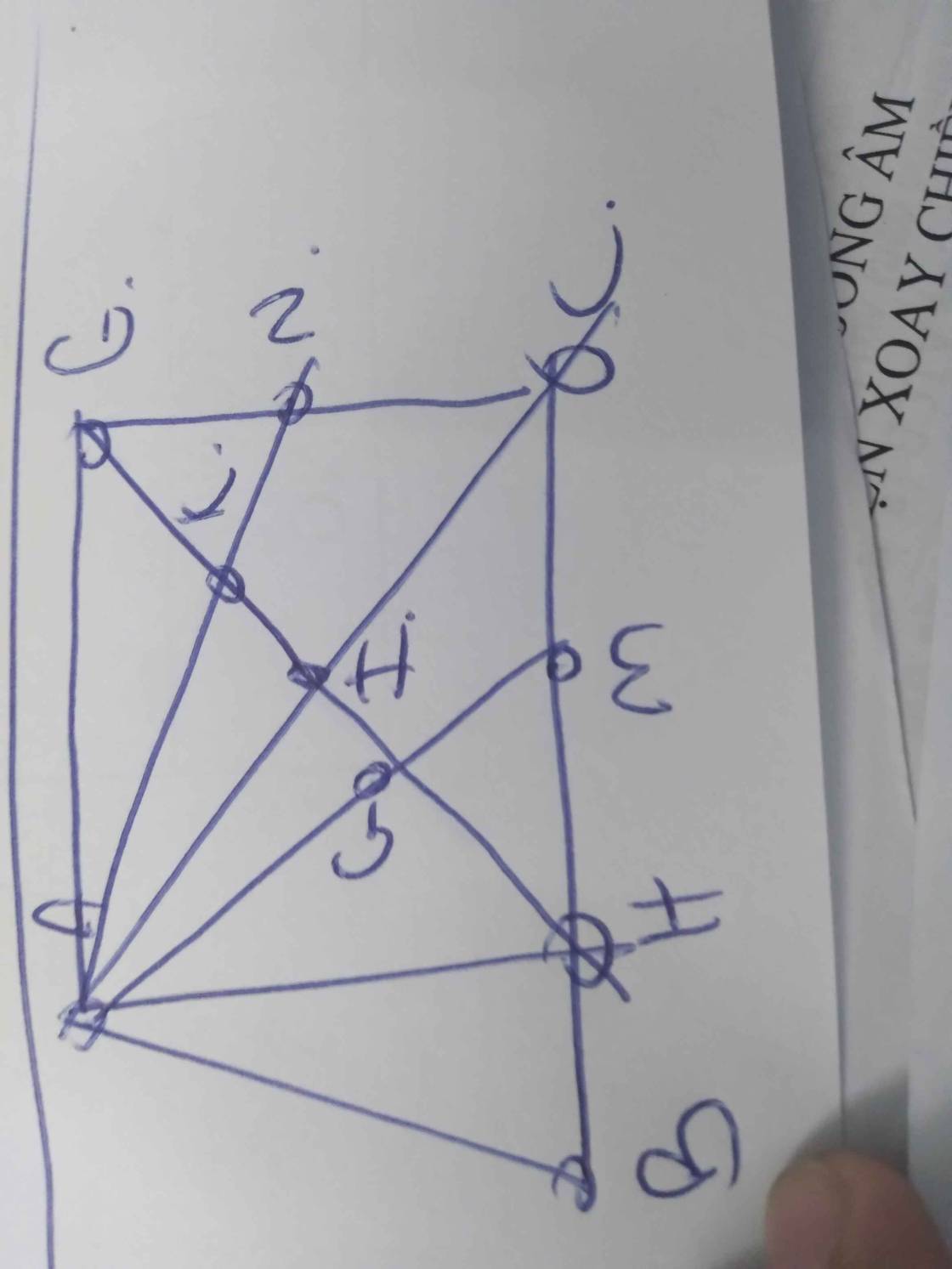

a, Xét tứ AHCE ta có: IH = IE ; IA = IC
⇒ tứ giácAHCE là hình bình hành (1)
Mà AH \(\perp\) BC \(\equiv\) H nên ⇒ \(\widehat{AHC}\) = 900 (2)
Kết hợp (1) và (2) ta có: Tứ giác AHCE là hình chữ nhật (đpcm).
b, Xét tam giác AHC có: M là trung điểm HC; I là trung điểm AC
⇒ AM; HI lần lượt là trung tuyến của tam giác AHC
⇒ G là trọng tâm của tam giác AHC ⇒ HG = \(\dfrac{2}{3}\)HI (3)
IG = HI - HG = HI - \(\dfrac{2}{3}\)HI = \(\dfrac{1}{3}\)HI
Chứng minh tương tự ta có: KE = \(\dfrac{2}{3}\)IE = \(\dfrac{2}{3}\)HI (4) ( vì IE = HI)
IK = IE - KE = IE - \(\dfrac{2}{3}\)IE = \(\dfrac{1}{3}\)IE = \(\dfrac{1}{3}\)HI (vì HI = IE)
GK = IG + IK = \(\dfrac{1}{3}\)HI + \(\dfrac{1}{3}\)HI = \(\dfrac{2}{3}\)HI (5)
Kết hợp(3); (4); (5) ta có: HG = GK = KE (đpcm)