Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Answer:
a,
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà đề ra: \(\widehat{A}=40^o\)
\(\widehat{B}=\widehat{C}\) (Tam giác ABC cân tại A)
\(\Rightarrow40^o+\widehat{B}+\widehat{B}=180^o\)
\(\widehat{2B}=140^o\)
\(\widehat{B}=70^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=70^o\)
b,
Theo đề ra: Tam giác ABC cân tại A
\(\Rightarrow\widehat{B}=\widehat{C}=50^o\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\widehat{A}+100^o=180^o\)
\(\Rightarrow\widehat{A}=80^o\)
c,
Theo đề ra: Tam giác ABC cân tại A
\(\Rightarrow\widehat{C}=\widehat{B}=60^o\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\widehat{A}+120^o=180^o\)
\(\Rightarrow\widehat{A}=60^o\)

Ta có tam giác ABC cân tại A
-> góc B = Góc C
mà góc B = 50 độ
-> góc C = 50 độ
Xét tam giác ABC có
góc A + góc B + góc C= 180 độ ( định lý tổng 3 góc trong tam giác)hay góc A + 50 + 50= 180 độ
góc A+ 100=180
góc A = 180-100
góc A = 80 độ
Xét tam giác ABC cân tại A có:
<B=<C=50 độ
=> <A= 180 độ -(<B+ <C)( Tổng 3 góc trong của tam giác)
=> <A= 180 độ -2.50 độ= 80 độ
P/S: cái "<" là chỉ góc nha bn

a, Vì △ABC cân tại A => \(\widehat{B}=\widehat{C}=\frac{180^o-\widehat{A}}{2}=\frac{180^o-40^o}{2}=\frac{140^o}{2}=70^o\)
b, Vì △ABC cân tại A => \(\widehat{B}=\widehat{C}=50^o\)
Xét △ABC có: \(\widehat{B}+\widehat{C}+\widehat{A}=180^o\)(tổng 3 góc trong tam giác)
\(\Rightarrow50^o+50^o+\widehat{A}=180^o\)\(\Rightarrow\widehat{A}=80^o\)
c, Vì △ABC cân tại A => \(\widehat{B}=\widehat{C}=60^o\)
Xét △ABC có: \(\widehat{B}+\widehat{C}+\widehat{A}=180^o\)(tổng 3 góc trong tam giác)
\(\Rightarrow60^o+60^o+\widehat{A}=180^o\)\(\Rightarrow\widehat{A}=60^o\)

c) Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{B}+\widehat{C}=180^0-40^0=140^0\)
Ta có: \(\widehat{B}:\widehat{C}=3:4\)(gt)
nên \(\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}\)
mà \(\widehat{B}+\widehat{C}=140^0\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}=\dfrac{\widehat{B}+\widehat{C}}{3+4}=\dfrac{140^0}{7}=20^0\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{\widehat{B}}{3}=20^0\\\dfrac{\widehat{C}}{4}=20^0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{B}=60^0\\\widehat{C}=80^0\end{matrix}\right.\)
Xét ΔABC có \(\widehat{A}< \widehat{B}< \widehat{C}\left(40^0< 60^0< 80^0\right)\)
mà cạnh đối diện với \(\widehat{A}\) là cạnh BC
cạnh đối diện với \(\widehat{B}\) là cạnh AC
và cạnh đối diện với \(\widehat{C}\) là cạnh AB
nên BC<AC<AB

Lời giải:
a)
Theo định lý tổng 3 góc trong tam giác:
$\widehat{D}+\widehat{E}+\widehat{F}=180^0$
$\Rightarrow \widehat{E}+\widehat{F}=180^0-\widehat{D}=180^0-60^0=120^0$
Mà tam giác $DEF$ cân tại $D$ nên $\widehat{E}=\widehat{F}$
Do đó:
$\widehat{E}=\widehat{F}=\frac{120^0}{2}=60^0$
b)
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$ (do $ABC$ cân tại $A$)
$\widehat{B}=\widehat{C}$ (do $ABC$ cân tại $A$)
$BM=CM$ (do $M là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.g.c)

a: \(\widehat{B}=\widehat{C}=\dfrac{180^0-56^0}{2}=62^0\)
b: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: ME=MF
hay ΔMEF cân tại M
d: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
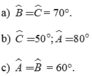

lỗi
Lỗi r bạn ;-;