Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

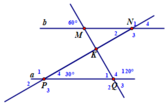
a. Q ^ 1 = 60 ° ( kề bù với Q ^ 4 ) mà Q 1 ^ đồng vị với M ^ = 60 ° => a//b
b. Vì a//b N 4 ^ = P ^ 4 = 30 ° ( đồng vị) ⇒ N ^ 1 = N ^ 3 = 150 ° ⇒ N ^ 4 = N ^ 2 = 130 °

Bài 1:
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=1\\2a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-2\end{matrix}\right.\)

đề bài đúng đây:
cho hình vẽ biết: x//y, biết góc M3= 50 độ. Tính góc M2, M4, N1, N2, N3 ?

Giải : a) Bước 1 : Gọi d \(\in\)ƯC ( a ; b ) , ta sẽ chứng minh rằng d \(\in\)ƯC ( 7a + 5b , 4a + 3b )
Thật vậy , a và b chia hết cho d nên 7a + 5b chia hết cho d , 4a + 3b chia hết cho d .
Bước 2 : Gọi d' \(\in\)ƯC ( 7a + 5b , 4a + 3b ) , ta sẽ chứng minh d' \(\in\)ƯC ( a ; b ) .
Thật vậy , 7a + 5b và 4a + 3b chia hết cho d' nên khử b , ta được 3 ( 7a + 5b ) - 5 ( 4a + 3b ) chia hết cho d' , tức là a chia hết cho d' ; khử a ta được 7 ( 4a + 3b ) - 4 ( 7a + 5b ) chia hết cho d' , tức là b chia hết cho d' . Vậy d' \(\in\)ƯC ( a ; b ) ,
Bước 3 : Kết luận A = B
b) Ta đã có A = B nên số lớn nhất thuộc A bằng số lớn nhất thuộc B , tức là ( a ; b ) = ( 7a + 5b , 4a + 3b ) ( ĐPCM )

11:
n^3-n^2+2n+7 chia hết cho n^2+1
=>n^3+n-n^2-1+n+8 chia hết cho n^2+1
=>n+8 chia hết cho n^2+1
=>(n+8)(n-8) chia hết cho n^2+1
=>n^2-64 chia hết cho n^2+1
=>n^2+1-65 chia hết cho n^2+1
=>n^2+1 thuộc Ư(65)
=>n^2+1 thuộc {1;5;13;65}
=>n^2 thuộc {0;4;12;64}
mà n là số tự nhiên
nên n thuộc {0;2;8}
Thử lại, ta sẽ thấy n=8 không thỏa mãn
=>\(n\in\left\{0;2\right\}\)
Để một tổng các số tự nhiên là số lẻ thì số lần xuất hiện số lẻ phải là một số lẻ.
Giả sử trong 10 số n1 , n2 , n3 ,..., n10 có 2k + 1 số lẻ
Vì bình phương số lẻ là số lẻ nên trong tổng S cũng có 2k + 1 số lẻ. Vậy S là một số lẻ.
Từ đó suy ra (S - 1) chia hết cho 2.