Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

5:
5.1: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
AB=AC
Do đó: ABDC là hình thoi
5.2: Xét tứ giác DMEC có
K là trung điểm chung của DE và MC
=>DMEC là hình bình hành
=>DM//ECvà DM=EC
mà AM=MD và A,M,D thẳng hàng
nên MA//EC và MA=EC
ΔABC cân tại A có AM là trung tuyến
nên AM vuông góc BC
Xét tứ giác AMCE có
AM//CE
AM=CE
góc AMC=90 độ
Do đó: AMCE là hình chữ nhật
5.3:
AMCE là hình chữ nhật
=>AE//CM và AE=CM
mà B,M,C thẳng và MB=MC
nên MB//AE và MB=AE
=>AEMB là hình bình hành
=>AM cắt EB tại trung điểm của mỗi đường
=>I là trung điểm của BE

a) Chứng minh được MBPD và BNDQ đều là hình bình hành Þ ĐPCM.
b) Áp dụng định lý Talet đảo cho DABD và DBAC tacos MQ//BD và MN//AC.
Mà ABCD là hình thoi nên AC ^ BD Þ MQ ^ MN
MNPQ là hình chữ nhật vì có các góc ở đỉnh là góc vuông
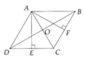

a:
ABCD là hình thoi
=>AC vuông góc BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại O và O là trung điểm chung của AC và BD
AM+MB=AB
PC+PD=DC
mà AM=PC và AB=DC
nên MB=PD
Xét tứ giác BMDP có
BM//DP
BM=DP
Do đó: BMDP là hình bình hành
b: Xét tứ giác AQCN có
AQ//CN
AQ=CN
Do đó: AQCN là hình bình hành
=>AC cắt QN tại trung điểm của mỗi đường
=>O là trung điểm của QN
=>N,O,Q thẳng hàng
c: Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD
=>MQ vuông góc AC
Xét ΔABC có
BM/BA=BN/BC
nên MN//AC
=>MQ vuông góc MN
BMDP là hình bình hành
=>BD cắt MP tại trung điểm của mỗi đường
=>O là trung điểm của MP
Xét tứ giác MNPQ có
O là trung điểm chung của MP và NQ
góc NMQ=90 độ
Do đó: MNPQ là hình chữ nhật

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
