

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Để hàm số \(y = \left( {m - 1} \right)x + m\) là hàm số bậc nhất thì \(m - 1 \ne 0 \Leftrightarrow m \ne 1\).
Vậy để hàm số \(y = \left( {m - 1} \right)x + m\) là hàm số bậc nhất thì \(m \ne 1\).
b) Ta có: \(y = 3 - 2mx = - 2mx + 3\)
Để hàm số \(y = - 2mx + 3\) là hàm số bậc nhất thì \( - 2m \ne 0 \Leftrightarrow m \ne 0\).
Vậy để hàm số \(y = 3 - 2mx\) là hàm số bậc nhất thì \(m \ne 0\).
a) \(y=\left(m-1\right)x+1\) là hàm số bậc nhất khi và chỉ khi
\(m-1\ne0\Leftrightarrow m\ne1\)
b) \(y=3-2mx\) là hàm số bậc nhất khi và chỉ khi
\(-2m\ne0\Leftrightarrow m\ne0\)

a) Để hàm số đã cho là hàm số bậc nhất thì:
3m + 5 ≠ 0
⇔ 3m ≠ -5
⇔ m ≠ -5/3
b) Để hàm số đã cho là hàm số bậc nhất thì:
2m² + 3 ≠ 0
⇔2m² ≠ -3 (luôn đúng)
Vậy m ∈ R
c) Để hàm số đã cho là hàm số bậc nhất thì:
m² - 3m = 0 và 3 - m ≠ 0
*) m² - 3m = 0
⇔ m(m - 3) = 0
⇔ m = 0 hoặc m - 3 = 0
**) m - 3 = 0
⇔ m = 3
*) 3 - m ≠ 0
⇔ m ≠ 3
Vậy m = 0 thì hàm số đã cho là hàm số bậc nhất
a: Để đây là hàm số bậc nhất thì 3m+5<>0
=>3m<>-5
=>\(m< >-\dfrac{5}{3}\)
b: Để đây là hàm số bậc nhất thì \(2m^2+3\ne0\)
mà \(2m^2+3>=3>0\forall m\)
nên \(m\in R\)
c: Để đây là hàm số bậc nhất thì \(\left\{{}\begin{matrix}m^2-3m=0\\3-m< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\left(m-3\right)=0\\m< >3\end{matrix}\right.\Leftrightarrow m=0\)

Câu 1: B
Câu 2: D
Bài 1: Các hàm số bậc nhất là
a: y=3x-2
a=3; b=-2
d: y=-2(x+5)
=-2x-10
a=-2; b=-10
e: \(y=1+\dfrac{x}{2}\)
\(a=\dfrac{1}{2};b=1\)
bạn ơi câu e minh viết là 1+x phần 2 bạn xem lai nha
câud mình viết thiếu là y = -2. (x+5) -4

ĐKXĐ: m ≠ 0 và m ≠ 3/2
a) Đồ thị hai hàm số đã cho là hai đường thẳng song song khi:
m = 3 - 2m
m + 2m = 3
3m = 3
m = 1 (nhận)
Vậy m = 1 thì đồ thị hai hàm số đã cho là hai đường thẳng song song
b) Đồ thị hai hàm số đã cho là hai đường thẳng cắt nhau khi
m ≠ 3 - 2m
m + 2m ≠ 3
3m ≠ 3
m ≠ 1
Vậy m ≠ 0; m ≠ 1 và m ≠ 3/2 thì đồ thị hai hàm số đã cho là hai đường thẳng cắt nhau

+ Với \(x = - 3\)\( \Rightarrow f\left( { - 3} \right) = 4.\left( { - 3} \right) - 1 = - 13;g\left( { - 3} \right) = - 0,5.\left( { - 3} \right) + 8 = 9,5\);
+ Với \(x = - 2\)\( \Rightarrow f\left( { - 2} \right) = 4.\left( { - 2} \right) - 1 = - 9;g\left( { - 2} \right) = - 0,5.\left( { - 2} \right) + 8 = 9\);
+ Với \(x = - 1\)\( \Rightarrow f\left( { - 1} \right) = 4.\left( { - 1} \right) - 1 = - 5;g\left( { - 1} \right) = - 0,5.\left( { - 1} \right) + 8 = 8,5\);
+ Với \(x = 0\)\( \Rightarrow f\left( 0 \right) = 4.0 - 1 = - 1;g\left( 0 \right) = - 0,5.0 + 8 = 8\);
+ Với \(x = 1\)\( \Rightarrow f\left( 1 \right) = 4.1 - 1 = 3;g\left( 1 \right) = - 0,5.1 + 8 = 7,5\);
+ Với \(x = 2\)\( \Rightarrow f\left( 2 \right) = 4.2 - 1 = 7;g\left( 2 \right) = - 0,5.2 + 8 = 7\);
+ Với \(x = 3\)\( \Rightarrow f\left( 3 \right) = 4.3 - 1 = 11;g\left( 3 \right) = - 0,5.3 + 8 = 6,5\).
Ta có bảng sau:
\(x\) | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
\(y = f\left( x \right) = 4x - 1\) | –13 | –9 | –5 | –1 | 3 | 7 | 11 |
\(y = g\left( x \right) = - 0,5x + 8\) | 9,5 | 9 | 8,5 | 8 | 7,5 | 7 | 6,5 |

a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
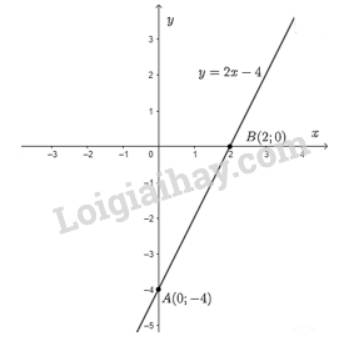
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).

Bài 2:
a: Thay x=1 và y=1 vào y=ax+5, ta được:
\(a\cdot1+5=1\)
=>a+5=1
=>a=-4
b: a=-4 nên y=-4x+5
| x | -2 | -1 | 0 | 1/2 | -3 |
| y=-4x+5 | 13 | 9 | 5 | 3 | -7 |
Bài 1:
a: \(y=-2\left(x+5\right)-4\)
\(=-2x-10-4\)
=-2x-14
a=-2; b=-14
b: \(y=\dfrac{1+x}{2}\)
=>\(y=\dfrac{1}{2}x+\dfrac{1}{2}\)
=>\(a=\dfrac{1}{2};b=\dfrac{1}{2}\)

câu 1,
a, 2(m-1)x +3 = 2m -5
<=> 2x (m-1) - 2m +8 = 0 (1)
Để PT (1) là phương trình bậc nhất 1 ẩn thì: m - 1 \(\ne\)0 <=> m\(\ne\)1
b, giải PT: 2x +5 = 3(x+2)-1
<=> 2x + 5 -3x -6 + 1 =0
<=> -x = 0
<=> x = 0
Thay vào (1) ta được: -2m + 8 =0
<=> -2m = -8
<=> m = 4 (t/m)
vậy m = 4 thì pt trên tương đương.................