Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

– Công thức cần sử dụng:
Đối với đoạn mạch mắc nối tiếp: R t đ = R 1 + R 2
Đối với đoạn mạch mắc song song:
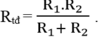
Khi R 1 nt R 2 ta có: R n t = R 1 + R 2 = 9 Ω ( 1 )
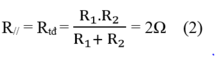

gọi R1,R2 lần lượt là x,y(ôm)
->hệ pt: \(\left\{{}\begin{matrix}x+y=100\\\dfrac{xy}{x+y}=16\end{matrix}\right.< =>\left\{{}\begin{matrix}y=100-x\left(1\right)\\\dfrac{x\left(100-x\right)}{x+100-x}=16\left(2\right)\end{matrix}\right.\)
giải pt(2)
\(=>\dfrac{100x-x^2}{100}=16< =>-x^2+100x-1600=0\)
\(\Delta=100^2-4\left(-1600\right)\left(-1\right)=3600>0\)
\(=>\left[{}\begin{matrix}x1=\dfrac{-100+60}{-2}=20\\x2=\dfrac{-100-60}{-2}=80\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}y1=80\\y2=20\end{matrix}\right.\)
vậy (R1;R2)={(20;80),(80;20)}

a) Điện trở tương đương là:
\(R_{tđ}=\dfrac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_2}}=\dfrac{1}{\dfrac{1}{20}+\dfrac{1}{30}}=12\left(\Omega\right)\)
b) Do mắc song song nên : \(U=U_1=U_2=36V\)
Cường độ dòng điện qua R1:
\(I_1=\dfrac{U_1}{R_1}=\dfrac{36}{20}=1,8\left(A\right)\)
Cường độ dòng điện qua R2:
\(I_2=\dfrac{U_2}{R_2}=\dfrac{36}{30}=1,2\left(A\right)\)
Cường độ dòng điện trong mạch chính:
\(I=I_1+I_2=1,8+1,2=3\left(A\right)\)
c) Do mắc nối tiếp nên:
\(R_{23}=R_2+R_3=30+40=70\left(\Omega\right)\)
Điện trở tương đương lúc này là:
\(R_{tđ}=\dfrac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_{23}}}=\dfrac{1}{\dfrac{1}{20}+\dfrac{1}{70}}=\dfrac{140}{9}\left(\Omega\right)\)
Bạn tự làm tóm tắt nhé!
Điện trở tương đương: \(R=\dfrac{R1.R2}{R1+R2}=\dfrac{20.30}{20+30}=12\Omega\)
\(U=U_1=U_2=36V\)(R1//R2)
Cường độ dòng điện qua mạch chính và mỗi điện trở:
\(I=\dfrac{U}{R}=\dfrac{36}{12}=3A\)
\(I_1=\dfrac{U1}{R1}=\dfrac{36}{20}=1.8A\)
\(I_2=\dfrac{U2}{R2}=\dfrac{36}{30}=1,2A\)
Điện trở tương đương lúc này: \(R_{td}=\dfrac{\left(R3+R2\right)R1}{R3+R2+R1}=\dfrac{\left(40+30\right)20}{40+30+20}=\dfrac{140}{9}\Omega\)

Mắc 4 điện trở 20Ω song song với nhau
Ta có: \(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_1}+\dfrac{1}{R_1}+\dfrac{1}{R_1}\)
\(\Leftrightarrow R_{tđ}=\dfrac{R_1R_1R_1R_1}{R_1R_1R_1+R_1R_1R_1+R_1R_1R_1+R_1R_1R_1}\)
\(\Leftrightarrow R_{tđ}=\dfrac{R_1^4}{4R_1^3}=\dfrac{20^4}{4.20^3}=5\left(\Omega\right)\)
Điện trở tương đương 1: Gọi sô hàng là m; số điện trở trên một hàng là n:
Ta có: \(R_{tđ}=\dfrac{n}{m}R_o\Leftrightarrow1=\dfrac{n}{m}.5\Leftrightarrow m=5n\)
Xét bảng:
số đt 1 hàng(n)
Ta thấy số hàng tỉ lệ thuân với số điện trở
nên số điện trở ít nhất là 5, đc mắc song song với nhau
Điện trở là 2:
P/S: Phương pháp trên(10 sử dụng xung đối; dưới này xung đối không đúng nên mk tạm gọi là "mò kim đáy bể" :)) cách giải thiachs thì ko bt :D
Dạng 3:
Điện trở tương đương 1: Gọi sô hàng là m; số điện trở trên một hàng là n:
Ta có: \(R_{tđ}=\dfrac{n}{m}R_o\Leftrightarrow3=\dfrac{n}{m}.5\Leftrightarrow3m=5n\)
Xét bảng:
số đt 1 hàng(n)
Ta thấy số hàng tỉ lệ thuân với số điện trở
nên số điện trở ít nhất là 15, đc mắc 5 hàng, mỗi hàng 3 điện trở
P/s: tự làm