Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi F là trung điểm của DC
E là trung điểm của AB
=>\(AE=EB=\dfrac{AB}{2}\)
F là trung điểm của DC
=>\(FD=FC=\dfrac{DC}{2}\)
mà AB=DC
nên AE=EB=CF=FD=AB/2
mà \(AD=BC=\dfrac{AB}{2}\)
nên \(AE=EB=CF=FD=AD=BC\)
Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
Hình bình hành AEFD có EA=AD
nên AEFD là hình thoi
=>EF=FD=DC/2
Xét ΔEDC có
EF là đường trung tuyến
\(EF=\dfrac{DC}{2}\)
Do đó: ΔEDC vuông tại E
=>DE\(\perp\)EC
b:
ABCD là hình bình hành
=>\(\widehat{BAD}+\widehat{ABC}=180^0\)
=>\(\widehat{ABC}=180^0-120^0=60^0\)
Xét ΔBEC có BE=BC và \(\widehat{B}=60^0\)
nên ΔBEC đều
=>\(\widehat{BEC}=60^0\)
\(\widehat{BEC}+\widehat{AEC}=180^0\)(hai góc kề bù)
=>\(\widehat{AEC}+60^0=180^0\)
=>\(\widehat{AEC}=180^0-60^0=120^0\)
Xét tứ giác AECD có
AE//CD
nên AECD là hình thang
Hình thang AECD có \(\widehat{EAD}=\widehat{AEC}\)
nên AECD là hình thang cân

a: Xét tứ giác ANMD có
AN//MD
AN=MD
Do đó: ANMD là hình bình hành
mà AN=AD
nên ANMD là hình thoi

a: Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó:AKCI là hình bình hành
Suy ra: AI//CK

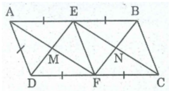
Ta có: Hình chữ nhật EMFN là hình thoi ⇒ ME = MF
ME = 1/2 DE (tính chất hình thoi)
MF = 1/2 AF (tính chất hình thoi)
Suy ra: DE = AF
⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)
⇒ ∠ A = 90 0 ⇒ Hình bình hành ABCD là hình chữ nhật.
Ngược lại: ABCD là hình chữ nhật ⇒ ∠ A = 90 0
Hình thoi AEFD có ∠ A = 90 0 nên AEFD là hình vuông
⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)
Hình chữ nhật EMFN là hình vuông (vì có 2 cạnh kề bằng nhau)
Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.