26
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 11 2021
\(7,\\ a,A=x^2-4x+3+11=\left(x-2\right)^2+10\ge10\\ \text{Dấu }"="\Leftrightarrow x=2\\ b,B=-\left(4x^2-4x+1\right)+6=-\left(2x-1\right)^2+6\le6\\ \text{Dấu }"="\Leftrightarrow x=\dfrac{1}{2}\\ c,x-y=2\Leftrightarrow x=y+2\\ \Leftrightarrow B=y^2-3x^2=y^2-3\left(y+2\right)^2\\ \Leftrightarrow B=y^2-3y^2-12y-12=-4y^2-12y-12\\ \Leftrightarrow B=-\left(4y^2+12y+9\right)-3=-\left(2y+3\right)^2-3\le-3\\ \text{Dấu }"="\Leftrightarrow y=-\dfrac{3}{2}\Leftrightarrow x=\dfrac{1}{2}\)
\(8,\\ \Leftrightarrow x^3-3x^2+5x+a=\left(x-2\right)\cdot a\left(x\right)\)
Thay \(x=2\Leftrightarrow8-12+10+a=0\Leftrightarrow a=-6\)
AH
Akai Haruma
Giáo viên
26 tháng 11 2021
Bài 7:
a.
$A=(x-1)(x-3)+11=x^2-4x+3+11=x^2-4x+14$
$=(x^2-4x+4)+10=(x-2)^2+10\geq 10$
Vậy gtnn của $A$ là $10$ khi $x=2$
b.
$B=5-4x^2+4x=6-(4x^2-4x+1)=6-(2x-1)^2\leq 6$
Vậy gtln của $B$ là $6$ khi $2x-1=0\Leftrightarrow x=\frac{1}{2}$
c.
$x-y=2\Rightarrow x=y+2$. Khi đó:
$B=y^2-3x^2=y^2-3(y+2)^2=y^2-(3y^2+12y+12)=-2y^2-12y-12$
$=6-2(y^2+6y+9)=6-2(y+3)^2\leq 6$
Vậy $B_{\max}=6$
AH
Akai Haruma
Giáo viên
26 tháng 11 2021
Bài 8:
Đặt $f(x)=x^3-3x^2+5x+a$
Theo định lý Bê-du, để $f(x)\vdots x-2$ thì $f(2)=0$
$\Leftrightarrow 6+a=0$
$\Leftrightarrow a=-6$
KN
23 tháng 8 2020
\(A=5-8x+x^2=-8x+x^2+6-11\)
\(=\left(x-4\right)^2-11\)
Vì \(\left(x-4\right)^2\ge0\forall x\)\(\Rightarrow\left(x-4\right)^2-11\ge-11\)
Dấu "=" xảy ra \(\Leftrightarrow\left(x-4\right)^2=0\Leftrightarrow x-4=0\Leftrightarrow x=4\)
Vậy Amin = - 11 <=> x = 4
KN
23 tháng 8 2020
\(B=\left(2-x\right)\left(x+4\right)=-x^2-2x+8\)
\(=-\left(x^2+2x+1\right)+9=-\left(x+1\right)^2+9\)
Vì \(\left(x+1\right)^2\ge0\forall x\)\(\Rightarrow-\left(x+1\right)^2+9\le9\)
Dấu "=" xảy ra \(\Leftrightarrow-\left(x+1\right)^2=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
Vậy Bmax = 9 <=> x = - 1
HH
2
N
22 tháng 11 2021
\(P=\left(x^2-4x+4\right)+\left(y^2+8y+16\right)+2021\\ P=\left(x-2\right)^2+\left(y+4\right)^2+2021\ge2021\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-4\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
22 tháng 11 2021
Lời giải:
$P(x)=x^2+y^2-4x+8y+2041=(x^2-4x+4)+(y^2+8y+16)+2021$
$=(x-2)^2+(y+4)^2+2021\geq 0+0+2021=2021$
Vậy $P(x)$ min = $2021$ khi $x-2=y+4=0$
$\Leftrightarrow x=2; y=-4$
KV
15 tháng 9 2023
a) x³ - 64x = 0
x(x² - 64) = 0
x(x - 8)(x + 8) = 0
x = 0 hoặc x - 8 = 0 hoặc x + 8 = 0
*) x - 8 = 0
x = 8
*) x + 8 = 0
x = -8
Vậy x = -8; x = 0; x = 8
b) x³ - 4x² = -4x
x³ - 4x² + 4x = 0
x(x² - 4x + 4) = 0
x(x - 2)² = 0
x = 0 hoặc (x - 2)² = 0
*) (x - 2)² = 0
x - 2 = 0
x = 2
Vậy x = 0; x = 2
c) x² - 16 - (x - 4) = 0
(x - 4)(x + 4) - (x - 4) = 0
(x - 4)(x + 4 - 1) = 0
(x - 4)(x + 3) = 0
x - 4 = 0 hoặc x + 3 = 0
*) x - 4 = 0
x = 4
*) x + 3 = 0
x = -3
Vậy x = -3; x = 4
d) (2x + 1)² = (3 + x)²
(2x + 1)² - (3 + x)² = 0
(2x + 1 - 3 - x)(2x + 1 + 3 + x) = 0
(x - 2)(3x + 4) = 0
x - 2 = 0 hoặc 3x + 4 = 0
*) x - 2 = 0
x = 2
*) 3x + 4 = 0
3x = -4
x = -4/3
Vậy x = -4/3; x = 2
e) x³ - 6x² + 12x - 8 = 0
(x - 2)³ = 0
x - 2 = 0
x = 2
f) x³ - 7x - 6 = 0
x³ + 2x² - 2x² - 4x - 3x - 6 = 0
(x³ + 2x²) - (2x² + 4x) - (3x + 6) = 0
x²(x + 2) - 2x(x + 2) - 3(x + 2) = 0
(x + 2)(x² - 2x - 3) = 0
(x + 2)(x² + x - 3x - 3) = 0
(x + 2)[(x² + x) - (3x + 3)] = 0
(x + 2)[x(x + 1) - 3(x + 1)] = 0
(x + 2)(x + 1)(x - 3) = 0
x + 2 = 0 hoặc x + 1 = 0 hoặc x - 3 = 0
*) x + 2 = 0
x = -2
*) x + 1 = 0
x = -1
*) x - 3 = 0
x = 3
Vậy x = -1; x = -1; x = 3
15 tháng 9 2023
Dòng cuối kết luận phải là \(\text{x }\in\text{ }\left\{-2;-1;3\right\}\) chứ ạ?
17 tháng 8 2021
a: Ta có: \(A=-x^2+2x+5\)
\(=-\left(x^2-2x-5\right)\)
\(=-\left(x^2-2x+1-6\right)\)
\(=-\left(x-1\right)^2+6\le6\forall x\)
Dấu '=' xảy ra khi x=1
b: Ta có: \(B=-x^2-8x+10\)
\(=-\left(x^2+8x-10\right)\)
\(=-\left(x^2+8x+16-26\right)\)
\(=-\left(x+4\right)^2+26\le26\forall x\)
Dấu '=' xảy ra khi x=-4
c: Ta có: \(C=-3x^2+12x+8\)
\(=-3\left(x^2-4x-\dfrac{8}{3}\right)\)
\(=-3\left(x^2-4x+4-\dfrac{20}{3}\right)\)
\(=-3\left(x-2\right)^2+20\le20\forall x\)
Dấu '=' xảy ra khi x=2
d: Ta có: \(D=-5x^2+9x-3\)
\(=-5\left(x^2-\dfrac{9}{5}x+\dfrac{3}{5}\right)\)
\(=-5\left(x^2-2\cdot x\cdot\dfrac{9}{10}+\dfrac{81}{100}-\dfrac{21}{100}\right)\)
\(=-5\left(x-\dfrac{9}{10}\right)^2+\dfrac{21}{20}\le\dfrac{21}{20}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{9}{10}\)
17 tháng 8 2021
e: Ta có: \(E=\left(4-x\right)\left(x+6\right)\)
\(=4x+24-x^2-6x\)
\(=-x^2-2x+24\)
\(=-\left(x^2+2x-24\right)\)
\(=-\left(x^2+2x+1-25\right)\)
\(=-\left(x+1\right)^2+25\le25\forall x\)
Dấu '=' xảy ra khi x=-1
f: Ta có: \(F=\left(2x+5\right)\left(4-3x\right)\)
\(=8x-6x^2+20-15x\)
\(=-6x^2-7x+20\)
\(=-6\left(x^2+\dfrac{7}{6}x-\dfrac{10}{3}\right)\)
\(=-6\left(x^2+2\cdot x\cdot\dfrac{7}{12}+\dfrac{49}{144}-\dfrac{529}{144}\right)\)
\(=-6\left(x+\dfrac{7}{12}\right)^2+\dfrac{529}{24}\le\dfrac{529}{24}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{7}{12}\)
2 tháng 9 2021
b: Ta có: \(B=x^2\left(11x-2\right)+x^2\left(x-1\right)-3x\left(4x^2-x-2\right)\)
\(=11x^3-2x^2+x^3-x^2-12x^3+3x^2+6x\)
\(=6x\)
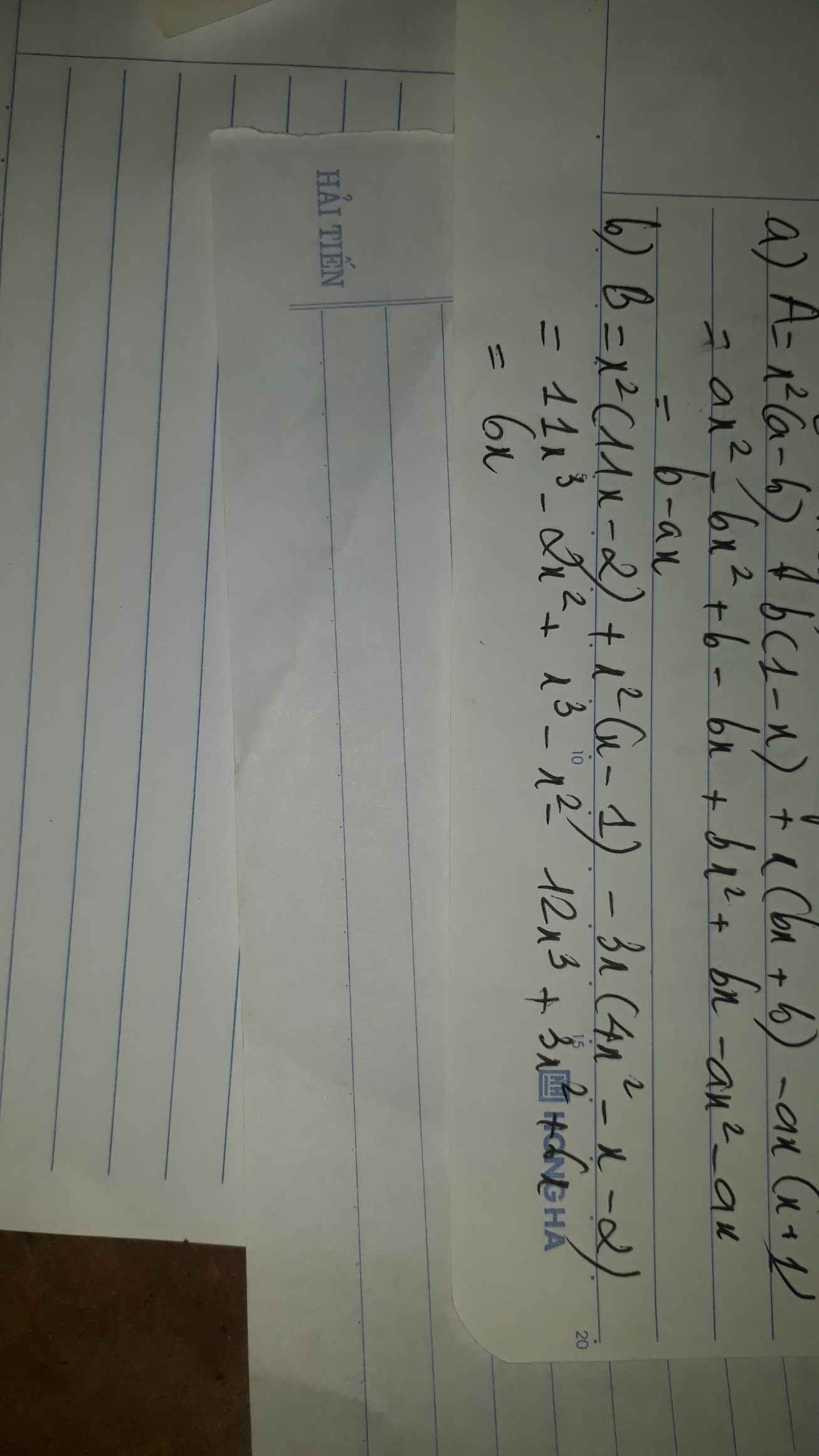
\(B=-\left(4x^2-4x+1\right)+6=-\left(2x-1\right)^2+6\le6\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)