
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có 3223 > 3222 = (32)111 = 9111. (1)
2332 < 2333 = (23)111 = 8111. (2)
Từ (1) và (2) suy ra: 2332 < 8111 < 9111 < 3223.
Vậy 2332 < 3223

`@` `\text {Ans}`
`\downarrow`
`a)`
\(3^{200}\text{ và }2^{300}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}\)
\(2^{300}=\left(2^3\right)^{100}=8^{100}\)
Vì `9 > 8 => 9^100 > 8^100`
`=> 3^200 > 2^300`
`b)`
\(27^{101}\text{ và }81^{35}\)
\(27^{101}=\left(3^3\right)^{101}=3^{303}\)
\(81^{35}=\left(3^4\right)^{35}=3^{140}\)
Vì `303 > 140 => 3^303 > 3^140`
`=> 27^101 > 81^35`
`c)`
\(2^{332}\text{ và }3^{223}\)
\(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)
Vì `9 > 8 => 9^111 > 8^111`
`=> 2^332 < 3^223.`
a: 3^200=9^100
2^300=8^100
mà 9>8
nên 3^200>2^300
b: 27^101=3^303
81^35=3^140
mà 303>140
nên 27^101>81^35
c: 2^332<2^333=8^111
3^223>3^222=9^111
mà 9>8
nên 3^223>8^111>2^332

Có cách chậm nhất à , ko có cách nhanh nhất
\(BCNN\left(38;88\right)\) = 1672
\(-\dfrac{13}{38}=-\dfrac{572}{1672}\)
\(-\dfrac{29}{88}=-\dfrac{551}{1672}\)
Ta có : \(-\dfrac{572}{1672}< -\dfrac{551}{1672}\)
\(\Rightarrow-\dfrac{13}{38}< -\dfrac{29}{88}\)

Hình vẽ:
Giải:
Xét tam giác ABH và tam giác DBH, ta có:
\(\widehat{AHB}=\widehat{DHB}=90^0\)
\(HA=HD\left(gt\right)\)
HB là cạnh chung
\(\Rightarrow\Delta ABH=\Delta DBH\) (Hai cạnh góc vuông)
Lại xét tam giác ACH và tam giác DCH, ta có:
\(\widehat{AHC}=\widehat{DHC}=90^0\)
\(HA=HD\left(gt\right)\)
HC là cạnh chung
\(\Rightarrow\Delta ACH=\Delta DCH\) (Hai cạnh góc vuông)
Chúc bạn học tốt!

a: Xét ΔABC có \(\widehat{B}>\widehat{C}\)
nên AB<AC
Xét ΔABC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
CH chung
HA=HD
Do đo; ΔAHC=ΔDHC
c: Xét ΔACB và ΔDCB có
CA=CD
\(\widehat{ACB}=\widehat{DCB}\)
CB chung
Do đó: ΔACB=ΔDCB
Suy ra: \(\widehat{BAC}=\widehat{BDC}=90^0\)
a: Xét ΔABC có ˆB>ˆCB^>C^
nên AB<AC
Xét ΔABC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
CH chung
HA=HD
Do đo; ΔAHC=ΔDHC
c: Xét ΔACB và ΔDCB có
CA=CD
ˆACB=ˆDCBACB^=DCB^
CB chung
Do đó: ΔACB=ΔDCB
Suy ra: ˆBAC=ˆBDC=900
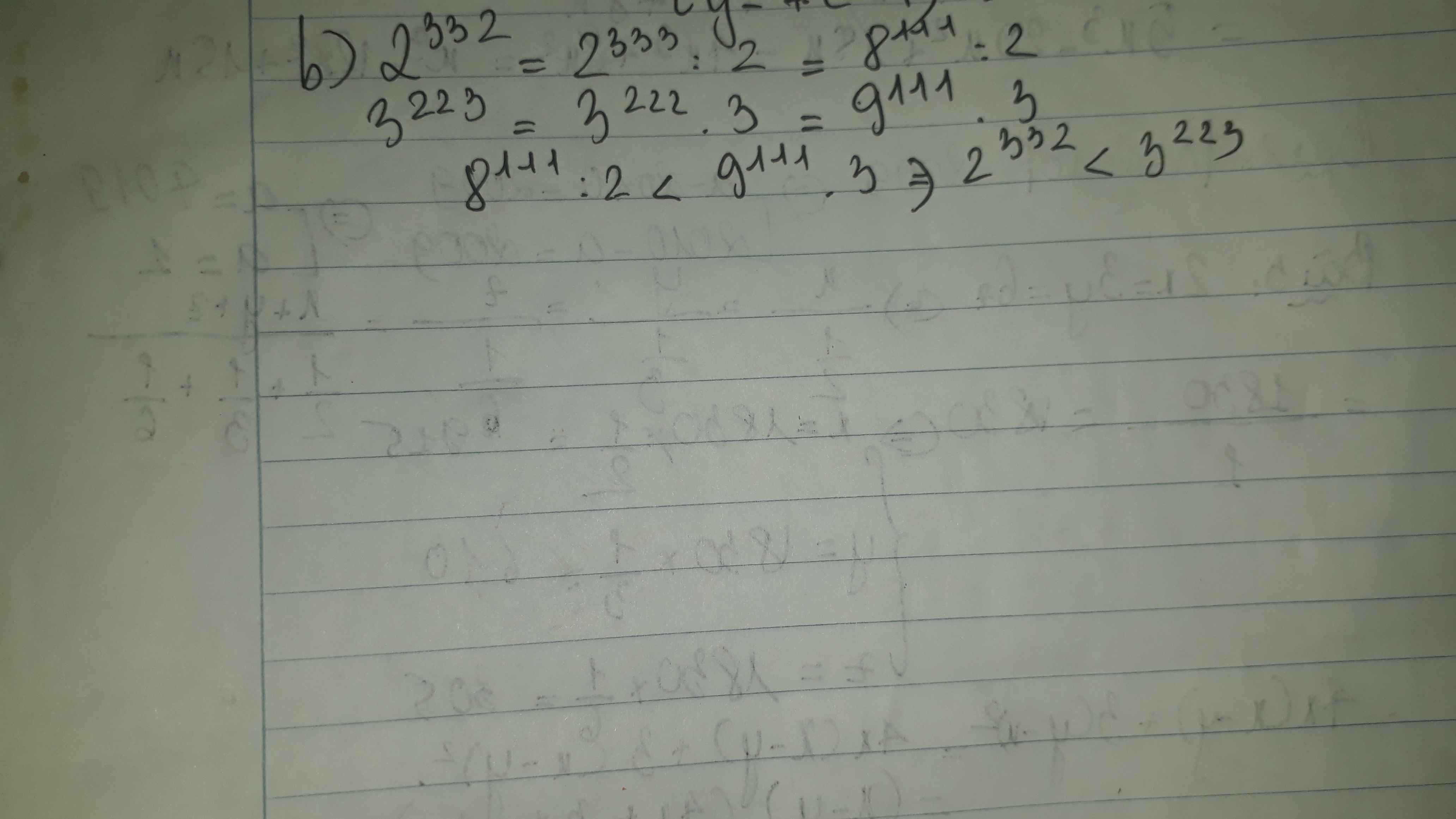

a) ta có: 34000 = (34)1000 = 811000
92000 = (92)1000 = 811000
=> ....
C2: ta có: 92000 = (32)2000= 34000
b) ta có: 2332 < 2333 = (23)111 = 8111
3223 > 3222 = (32)111 = 9111
=> 8111 < 9111
=> 2332 < 3223