K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 11 2023
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{4;9\right\}\end{matrix}\right.\)
\(A=\left(\dfrac{x-3\sqrt{x}}{x-9}-1\right):\left(\dfrac{9-x}{x+\sqrt{x}-6}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-1\right):\left(\dfrac{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-1\right):\left(\dfrac{3-x+\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+3}\right)\)
\(=\dfrac{\sqrt{x}-\sqrt{x}-3}{\sqrt{x}+3}:\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+3}\)
\(=\dfrac{-3}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{-\left(\sqrt{x}-2\right)}=\dfrac{3}{\sqrt{x}-2}\)
b: A<1
=>A-1<0
=>\(\dfrac{3-\sqrt{x}+2}{\sqrt{x}-2}< 0\)
=>\(\dfrac{\sqrt{x}-5}{\sqrt{x}-2}>0\)
TH1: \(\left\{{}\begin{matrix}\sqrt{x}-5>0\\\sqrt{x}-2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}>5\\\sqrt{x}>2\end{matrix}\right.\Leftrightarrow\sqrt{x}>5\)
=>x>25
TH2: \(\left\{{}\begin{matrix}\sqrt{x}-5< 0\\\sqrt{x}-2< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}< 2\\\sqrt{x}< 5\end{matrix}\right.\)
=>\(\sqrt{x}< 2\)
=>0<=x<4
AA
6 tháng 8 2021
a, A= \(\frac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}:\left(\frac{\left(\sqrt{x}\right)^2}{\sqrt{x}\left(\sqrt{x}+2\right)}+\frac{x}{\sqrt{x}+2}\right)\)
A=\(\frac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}:\left(\frac{\sqrt{x}}{\left(\sqrt{x}+2\right)}+\frac{x}{\sqrt{x}+2}\right)\)
A=\(\frac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}:\left(\frac{\sqrt{x}+x}{\left(\sqrt{x}+2\right)}\right)\)
A=\(\frac{1}{x+2\sqrt{x}}\)
b, A >= \(\frac{1}{3\sqrt{x}}\)
=> \(\frac{1}{x+2\sqrt{x}}\) >= \(\frac{1}{3\sqrt{x}}\)
=> x <= -1 , x >= 4 (x khác 0)
31 tháng 7 2023
a:
Sửa đề: \(P=\left(\dfrac{3+x}{3-x}-\dfrac{3-x}{3+x}-\dfrac{4x^2}{x^2-9}\right):\left(\dfrac{5}{3-x}-\dfrac{4x+2}{3x-x^2}\right)\)\(P=\left(\dfrac{-\left(x+3\right)}{x-3}+\dfrac{x-3}{x+3}-\dfrac{4x^2}{\left(x-3\right)\left(x+3\right)}\right):\dfrac{5x-4x-2}{x\left(3-x\right)}\)
\(=\dfrac{-x^2-6x-9+x^2-6x+9-4x^2}{\left(x-3\right)\left(x+3\right)}:\dfrac{x-2}{x\left(3-x\right)}\)
\(=\dfrac{-4x^2-12x}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x\left(3-x\right)}{x-2}\)
\(=\dfrac{-4x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{-x\left(x-3\right)}{x-2}=\dfrac{4x^2}{x-2}\)
b: x^2-4x+3=0
=>x=1(nhận) hoặc x=3(loại)
Khi x=1 thì \(P=\dfrac{4\cdot1^2}{1-2}=-4\)
c: P>0
=>x-2>0
=>x>2
d: P nguyên
=>4x^2 chia hết cho x-2
=>4x^2-16+16 chia hết cho x-2
=>x-2 thuộc {1;-1;2;-2;4;-4;8;-8;16;-16}
=>x thuộc {1;4;6;-2;10;-6;18;-14}
AH
Akai Haruma
Giáo viên
28 tháng 10 2021
Lời giải:
a. ĐKXĐ: $x>0; x\neq 4$
\(M=\frac{x}{\sqrt{x}(\sqrt{x}-2)}-\frac{4\sqrt{x}-4}{\sqrt{x}(\sqrt{x}-2)}=\frac{x-(4\sqrt{x}-4)}{\sqrt{x}(\sqrt{x}-2)}=\frac{x-4\sqrt{x}+4}{\sqrt{x}(\sqrt{x}-2)}=\frac{(\sqrt{x}-2)^2}{\sqrt{x}(\sqrt{x}-2)}=\frac{\sqrt{x}-2}{\sqrt{x}}\)
b.
\(x=3+2\sqrt{2}=(\sqrt{2}+1)^2\Rightarrow \sqrt{x}=\sqrt{2}+1\)
\(M=\frac{\sqrt{x}-2}{\sqrt{x}}=\frac{\sqrt{2}+1-2}{\sqrt{2}+1}=3-2\sqrt{2}\)
c.
$M>0\Leftrightarrow \frac{\sqrt{x}-2}{\sqrt{x}}>0$
$\Leftrightarrow \sqrt{x}-2>0$
$\Leftrightarrow \sqrt{x}>2\Leftrightarrow x>4$
Kết hợp đkxđ suy ra $x>4$
26 tháng 7 2021
a) Ta có: \(P=\left(\dfrac{1}{1-\sqrt{a}}-\dfrac{1}{1+\sqrt{a}}\right)\cdot\left(1-\dfrac{1}{\sqrt{a}}\right)\)
\(=\dfrac{1+\sqrt{a}-1+\sqrt{a}}{-\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\cdot\dfrac{\sqrt{a}-1}{\sqrt{2}}\)
\(=\dfrac{-2}{\sqrt{a}+1}\)
b) Ta có: \(P=\dfrac{-1}{2}\)
nên \(\dfrac{2}{\sqrt{a}+1}=\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{a}+1=4\)
\(\Leftrightarrow a=9\)(thỏa ĐK)
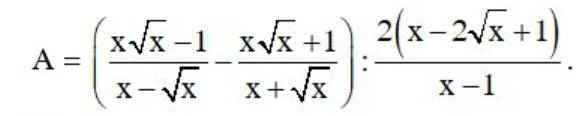
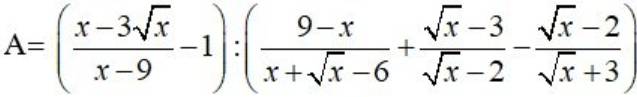
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x< >1\end{matrix}\right.\)
\(A=\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right):\dfrac{2\left(x-2\sqrt{x}+1\right)}{x-1}\)
\(=\left(\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{x-1}{2\left(\sqrt{x}-1\right)^2}\)
\(=\left(\dfrac{x+\sqrt{x}+1}{\sqrt{x}}-\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\right)\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{2\left(\sqrt{x}-1\right)^2}\)
\(=\dfrac{x+\sqrt{x}+1-x+\sqrt{x}-1}{\sqrt{x}}\cdot\dfrac{\left(\sqrt{x}+1\right)}{2\left(\sqrt{x}-1\right)}\)
\(=\dfrac{2\left(\sqrt{x}+1\right)}{2\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b: Để A<0 thì \(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}< 0\)
=>\(\sqrt{x}-1< 0\)
=>\(\sqrt{x}< 1\)
=>0<x<1
\(A=\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right):\dfrac{2\left(x-2\sqrt{x}+1\right)}{x-1}\left(đkxđ:x>0;x\ne1\right)\\ =\left(\dfrac{\left(\sqrt{x}\right)^3-1^3}{\sqrt{x}\left(\sqrt{x-1}\right)}-\dfrac{\left(\sqrt{x}\right)^3+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{x-1}{2\left(\sqrt{x}-1\right)^2}\\ =\left(\dfrac{\left(\sqrt{x}-1\right)\left(x+2\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(x-2\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}\\ =\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}\\ =\dfrac{4\sqrt{x}}{\sqrt{x}}\cdot\dfrac{\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}\\ =\dfrac{2\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
`b,` Để `A<0` thì :
\(\dfrac{2\left(\sqrt{x}+1\right)}{\sqrt{x}-1}< 0\\ \Leftrightarrow\sqrt{x}-1< 0\left(vì.2\left(\sqrt{x}+1\right)>0\right)\\ \Leftrightarrow\sqrt{x}< 1\\ \Leftrightarrow0\le x< 1\)
Kết hợp với điều kiện xác định ta có : \(0< x< 1\)