Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(T_1=20^oC=293K\)
\(T_2=42^oC=315K\)
Áp suất săm xe khi để ở nhiệt độ \(42^oC\). Quá trình đẳng tích:
\(\dfrac{p_1}{T_1}=\dfrac{p_2}{T_2}\Rightarrow\dfrac{2}{293}=\dfrac{p_2}{315}\)
\(\Rightarrow p_2=2,15atm< p_{max}=2,5atm\)
Vậy săm xe không bị nổ.

Thể tích của bơm:
V = s . h = π d 2 4 . h = 3 , 14. h 2 4 .50
= 981 , 25 c m 3
Gọi n là số lần bơm để không khí đưa vào săm có áp suất p 1 và thể tích V 1 .
Ta có: p = p 1 + p 0 hay
p 1 = p − p o = ( 5 − 1 ) 10 5 = 4.10 5 N / m 2 .
Theo định luật Bôi-lơ – Ma-ri-ốt:
n p o V o = p 1 V 1 hay
n = p 1 V 1 p o V o = 4.10 5 .7.10 3 10 5 .981 , 25 ≈ 29 lần.
Cứ 1 lần bơm mất thời gian là 2,5s
⇒ 29 lần bơm mất thời gian là t = 72,5s

Đáp án: A
Ta có:
- Trạng thái 1: T 1 = 20 + 273 = 293 K p 1 = 2 a t m
- Trạng thái 2: T 2 = 42 + 273 = 315 K p 2 = ?
Áp dụng biểu thức định luật Sáclơ, ta có:
p 1 T 1 = p 2 T 2 → p 2 = T 2 p 1 T 1 = 315 2 293 = 2,15 a t m
Nhận thấy: p 2 < p m a x → bánh xe không bị nổ

Chọn C.
Áp suất trong bánh xe khi bơm xong: p = p0 + p’
Với p’ = F/S = 350/0,005 = 0,7.105 Pa;
→ p = 1,7.105 Pa lớn hơn 1,5p0 nên thể tích sau khi bơm là 2000 cm3.
Mỗi lần bơm có 8.25 = 200 cm3 không khí ở áp suất p0 được đưa vào bánh xe. Sau n lần bơm có 200n cm3 không khí được đưa vào bánh. Ban đầu có 1500 cm3 không khí ở áp suất p0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p1 = p0; V1 = (1500 + 200n)
Trạng thái 2: p2 = 1,7.105 Pa; V2 = 2000 cm3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần

Gọi F là trọng lượng của xe, V 0 là thế tích mỗi lần bơm, V thể tích săm xe
Ta có trong lần bơm đầu tiên:


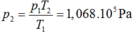
Đáp án B
Xét khối khí bên trong chiếc săm
Gọi P o là áp suất của khối khí khi ở nhiệt độ
Gọi P là áp suất của khối khí khi nó được đặt ở nhiệt độ 400C
Vì thể tích của khối khí không đổi, nên theo định luật Saclo, ta co