
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}=\overrightarrow{0}\Leftrightarrow\overrightarrow{CG}=-\overrightarrow{AG}-\overrightarrow{BG}\)
\(\Rightarrow\overrightarrow{AB}+\overrightarrow{CG}=\overrightarrow{AB}-\overrightarrow{AG}-\overrightarrow{BG}=\overrightarrow{GB}-\overrightarrow{BG}=2\overrightarrow{GB}\)
\(\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{CG}\right|=2GB\)
Gọi BN là đường cao của tam giác ABC
Theo Pythagoras:\(BN^2=BC^2-\left(\dfrac{AB}{2}\right)^2=4a^2-a^2=3a^2\Rightarrow BN=\sqrt{3}a\)
Vì BN là đường cao trong tam giác đều nên cũng là đường trong tuyến trong tam giác đều \(\Rightarrow GB=\dfrac{2}{3}BN=\dfrac{2}{3}\cdot\sqrt{3}a=\dfrac{2\sqrt{3}}{3}a\)
\(\Rightarrow\left|\overrightarrow{AB}+\overrightarrow{CG}\right|=\dfrac{4\sqrt{3}}{3}a\)

Câu 1: B
Câu 2: C
Câu 3: A
Câu 4: D
Câu 5: B
Câu 6: D
Câu 7: A

Đặt \(\sqrt{\dfrac{x^2}{x-3}}=a\left(a>=0\right)\)
Theo đề, ta có bất phương trình:
\(a^2>2a+8\)
=>(a-4)(a+2)>0
=>a-4>0
\(\Leftrightarrow\dfrac{x^2}{x-3}>16\)
\(\Leftrightarrow x^2-16x+48>0\)
\(\Leftrightarrow x\in R\)
Vậy: S=R\{3}

`\sqrt{8+2x-x^2}+3x>6`
`đkxđ:-2<=x<=4`
`bpt<=>\sqrt{8+2x-x^2}>6-3x`
Đp bp 2 vế:`x<=2`
`<=>8+2x-x^2>9x^2-36x+36`
`<=>10x^3-38x+28<0`
`<=>5x^2-19x+14<0`
`<=>(x-1)(5x-14)<0`
`<=>1<x<14/5`
Kết hợp đkxđ:
`1<x<=2`
`=>S=(1,2]`
`=>ab=2`
`=>` chọn A

Ở đây chỉ thấy các câu 26, 32, 34, 36
26.
\(S_{ABC}=\dfrac{1}{2}AB^2=\dfrac{a^2}{18}\)
\(BC=AB\sqrt{2}=\dfrac{a\sqrt{2}}{3}\Rightarrow p=\dfrac{AB+AC+BC}{2}=\dfrac{2a+a\sqrt{2}}{6}\)
\(\Rightarrow r=\dfrac{S}{p}=\dfrac{6a^2}{18a\left(2+\sqrt{2}\right)}=\dfrac{\left(2-\sqrt{2}\right)a}{6}\)
32.
Đường thẳng nhận \(\overrightarrow{n}=\left(5;-1\right)\) là 1 vtpt
34.
Áp dụng định lý hàm cos:
\(c=\sqrt{a^2+b^2-2ab.cosC}=\sqrt{8^2+7^2-2.8.7.cos60^0}=\sqrt{57}\)
36.
\(y=\sqrt{\dfrac{x^2-2mx+5m}{2021}}\)
Hàm xác định trên R khi và chỉ khi: \(x^2-2mx+5m\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-5m\le0\Rightarrow0\le m\le5\)
Có 5 giá trị nguyên dương của m thỏa mãn (1;2;3;4;5)




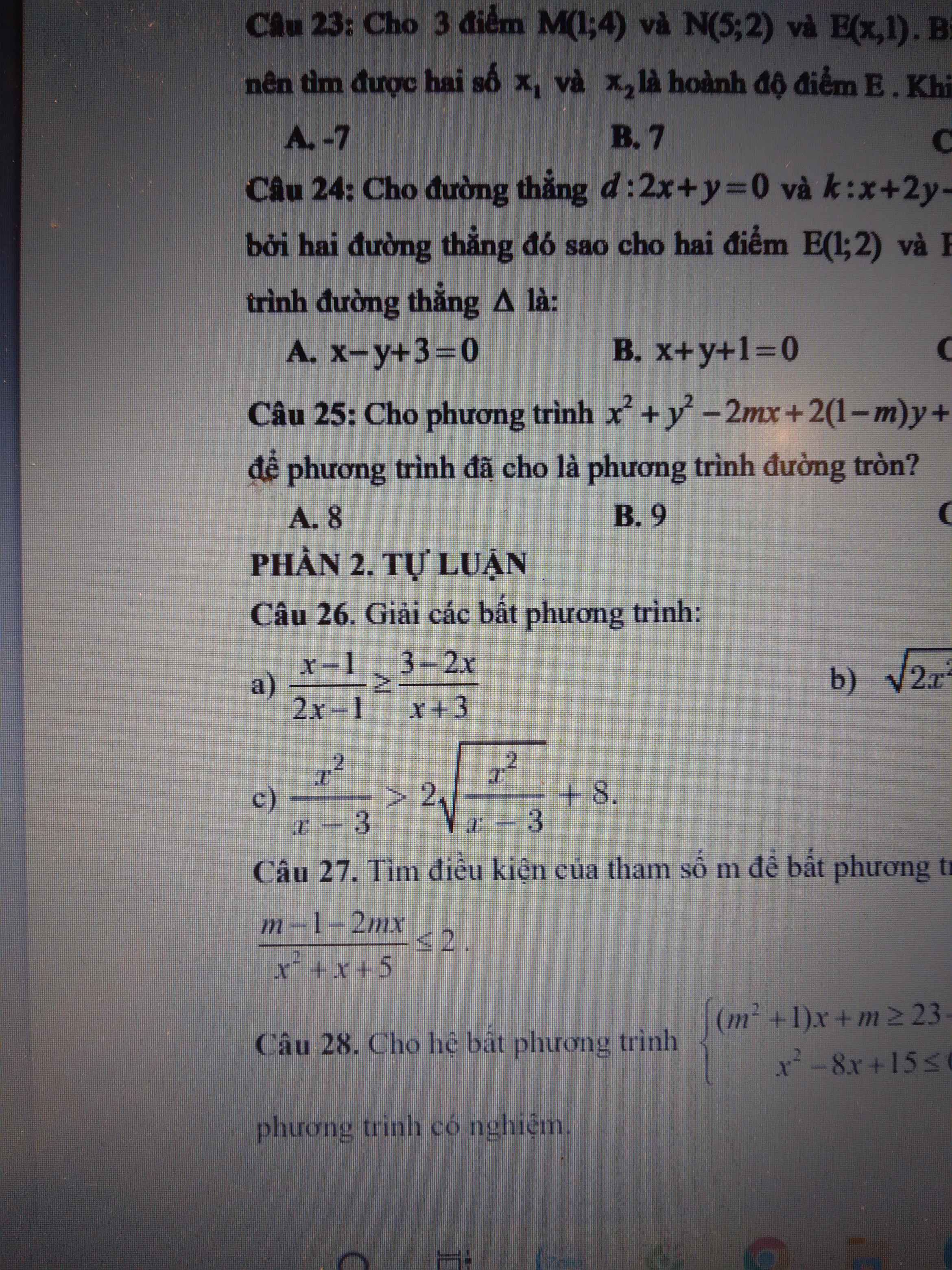



b
Bn có thể viết lược giải ra luôn ko