Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
HD Giải:
Ta có: khoảng cách ngắn nhất giữa hai gợn lồi liên tiếp là 2cm → λ/2 = 2 → λ = 4cm
Hai nguồn ngược pha, nên điểm dao động với biên độ cực đại phải thỏa mãn: d2 – d1 = (k + 0,5)λ
Điểm dao động với biên độ cực tiểu thỏa mãn: d2 – d1 = k.λ
Số gợn lồi và lõm xuất hiện giữa hai điểm S1S2 là:
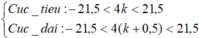
<=> 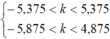
<=> 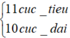

Đáp án: C
HD Giải: λ = v f = 60 100
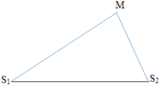
Điểm dao động với biên độ cực đại trên đoạn MS1 thỏa mãn:
![]()
<=> ![]()
<=> ![]()
có 6 cực đại trên MS1

Khi hệ vân giao thoa đã ổn định thì trung điểm I của S 1 S 2 lại luôn luôn là cực đại giao thoa. Do đó, ta phải có :
S 1 I = S 2 I = k λ /2 + λ /4 = (2k + 1) λ /4
S 1 S 2 = 2 S 1 I = (2k + 1) λ /2
Ban đầu ta đã có : S 1 S 2 = 8cm = 10 λ = 20 λ /2
Vậy chỉ cần tăng khoảng cách S 1 , S 2 thêm λ /2 tức là 0,4 cm.
Khi đó nếu không kể đường trung trực của S 1 S 2 thì có 20 gợn sóng hình hypebol (vì gợn sóng là quỹ tích những điểm dao động mạnh hơn cả).

Đáp án A
Bước sóng: λ = v.T = v/f = 80/40 = 2cm
=> Khoảng cách ngắn nhất giữa hai điểm cực đại giao thoa trên đoạn thẳng S1S2 là λ/2 = 1cm

Bước sóng: \(\lambda=\frac{v}{f}=\frac{80}{100}=0,8\)(cm).
M2 cùng pha với M1 nên: \(d_2-d_1=k\lambda\)
Do M2 gần M1 nhất nên \(k=\pm1\Rightarrow d_2-d_1 =\pm0,8\)cm.
TH1: k=1 \(\Rightarrow d_2-d_1=0,8 \Rightarrow d_2=8,8\)cm \(\Rightarrow x= M_2O-M_1O=\sqrt{8,8^2-4^2}-\sqrt{8^2-4^2}=0,91\)cm.
TH1: k=-1 \(\Rightarrow d_2-d_1=-0,8 \Rightarrow d_2=7,2\)cm \(\Rightarrow x= M_2O-M_1O=\sqrt{8^2-4^2}-\sqrt{7,2^2-4^2}=0,94\)cm.
Như vậy x nhỏ nhất ứng với TH1, khi đó M2 cách M1 khoảng nhỏ nhất là 0,91cm.
Đáp án: A
Bạn cho mình hỏi tại sao M2 cùng pha với M1 thì: d2 - d1 = k\(\lambda\)

Đáp án C
+ Gọi I là điểm nằm trên MN và cách các nguồn khoảng d. Theo bài ta có d M = 8 ; d N = 16
+ Độ lệch pha của I so với hai nguồn là
∆ φ = 2 π d λ = 2 k π ⇒ d = k λ

Suy ra, k = 6; 7; 8; 9; 10.
Vậy trên MN có 5 điểm dao động cùng pha với hai nguồn.

Bước sóng của sóng : λ = v/f = 120/20 = 6cm. S 1 S 2 = 18cm = 6 λ /2. Trừ hai điểm S 1 , S 2 thì trên đoạn thẳng S 1 S 2 có 5 điểm, tại đó mặt nước dao động mạnh nhất.
Vậy : "Nếu không tính gợn sóng thẳng trùng với đường trung trực của S 1 S 2 thì có 4 gợn sóng hình hypebol".

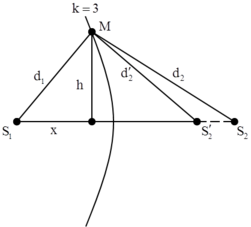
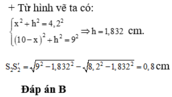
Bước sóng: \(\lambda=v/f=120/100=1,2(cm)\)
Số gợn sóng quan sát đc là: \(2.[\dfrac{S_1S_2}{\lambda}]+1=17\)
Tuy nhiện, vì 9,6 chia hết cho 1,2 nên ta trừ đi 2 điểm ở đầu mút, do vậy số gợn sóng quan sát đc là:
17-2=15 (gợn sóng)
cho mình hỏi sao 9,6 chia hết cho 1,2 thì lại trừ đi 2, chứ k phải là vì giữa S1S2 nên trừ đi 2 đầu mút à