
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Đặt $2x=t$ thì bài toán trở thành tìm max, min của $y=3\sin t$ với $t\in [0;\pi]$
Với mọi $t\in [0;\pi]$ thì $\sin t\in [0;1]$ (cái này bạn có thể xem lại đồ thị hàm sin)
$\Rightarriw y=3\sin t\in [0;3]$ hay $y_{\min}=0; y_{\max}=3$

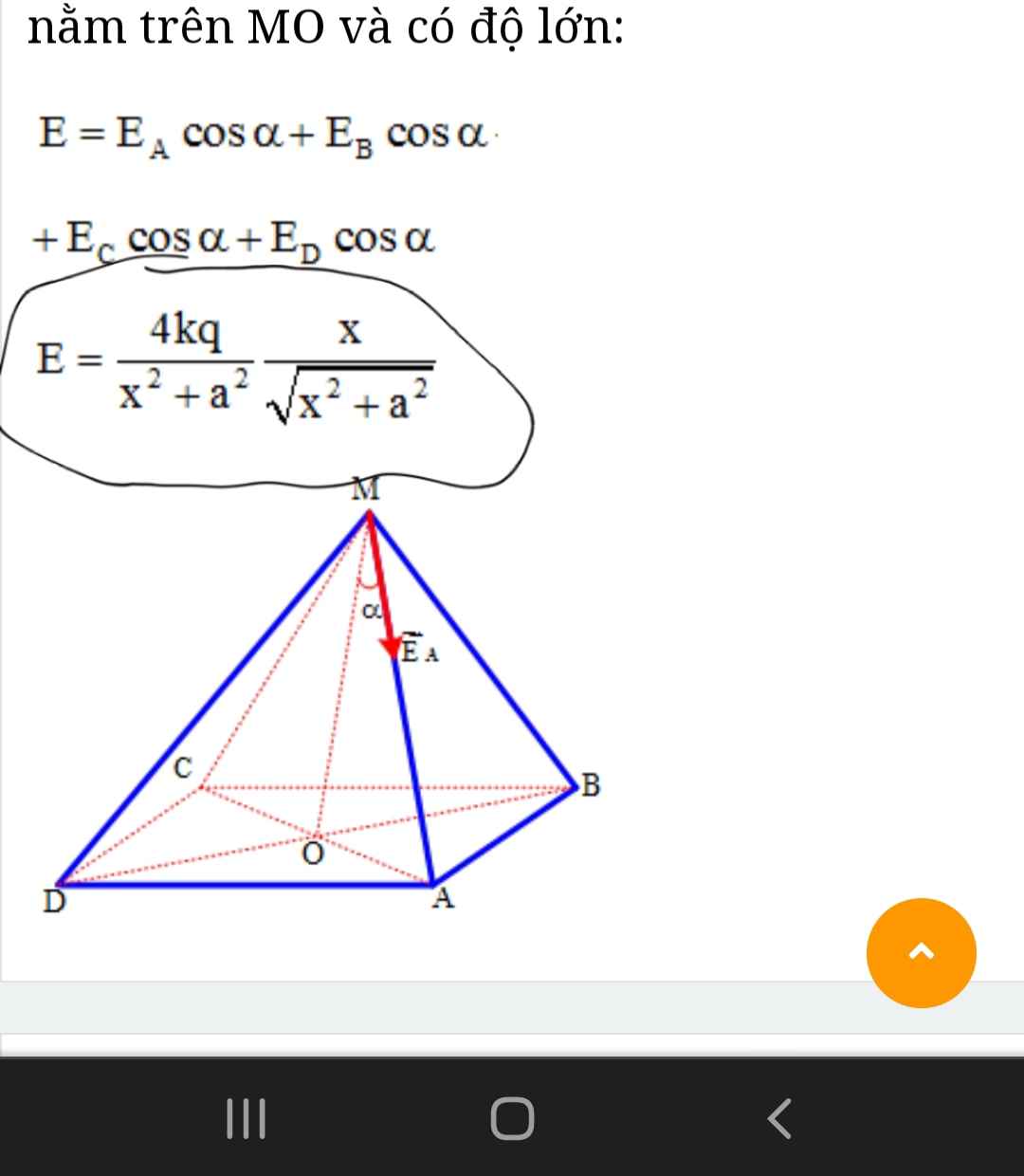
\(\dfrac{4kq.x}{\sqrt{\left(x^2+a^2\right)^3}}=\dfrac{4kq.x}{\sqrt{\left(x^2+\dfrac{a^2}{2}+\dfrac{a^2}{2}\right)^3}}\le\dfrac{4kq.x}{\sqrt{\dfrac{27.x^2.a^4}{4}}}=\dfrac{4kq.x}{\dfrac{3\sqrt{3}}{2}.x.a^2}=\dfrac{8\sqrt{3}.kq}{9a^2}\)
Dấu "=" xảy ra khi \(x=\dfrac{a}{\sqrt{2}}\)

\(I\left(\dfrac{1}{2};\dfrac{3}{4}\right)\)
Nhìn BBT ta thấy \(y_{max}=3\) còn \(y_{min}=\dfrac{3}{4}\)
Thầy ơi, tại sao từ đỉnh y mà lại suy ra được Min và max vậy ạ,mong thầy trả lời

Bạn mk khen hok đc chứ mk hok Vinastudy, Vinastudy dạy cũng hay lắm bạn à.

em em em em ,em blink này
chớp mắt