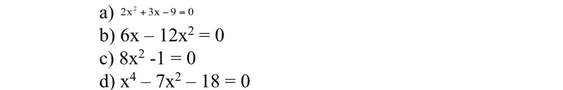Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1) Với x=4 thì
\(A=\dfrac{2\sqrt{4}}{\sqrt{4}+3}=\dfrac{4}{2+3}=\dfrac{4}{5}\)
2) \(P=A+B\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{11\sqrt{x}-3}{x-9}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)+11\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x+3}\right)}\)
\(=\dfrac{2x-6\sqrt{x}+x+4\sqrt{x}+3+11\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-3}\)
3) Để P< 3 thì
\(\dfrac{3\sqrt{x}}{\sqrt{x}-3}< 3\)
\(\Leftrightarrow\dfrac{3\sqrt{x}}{\sqrt{x}-3}-\dfrac{3\left(\sqrt{x}-3\right)}{\sqrt{x}-3}< 0\)
\(\Leftrightarrow\dfrac{9}{\sqrt{x}-3}< 0\)
\(\Rightarrow\sqrt{x}-3< 0\) ( vì 9>0)
<=> x<9
Vậy giá trị nguyên lớn nhất của x để P <3 là 8

\(\dfrac{1}{\sqrt[3]{4}+\sqrt[3]{2}+1}=\dfrac{\sqrt[3]{2}-1}{\left(\sqrt[3]{2}-1\right)\left(\sqrt[3]{4}+\sqrt[3]{2}+1\right)}\)
\(=\dfrac{\sqrt[3]{2}-1}{2-1}=\sqrt[3]{2}-1\)

Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{1}{2}\\x_1x_2=-2\end{matrix}\right.\)
\(A=3-x_1^2-x_2^2\\ =3-\left(x_1^2+x_2^2\right)\\ =3-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =3-\left[\left(-\dfrac{1}{2}\right)^2-2.\left(-2\right)\right]\\ =3-\left(\dfrac{1}{4}+4\right)\\ =3-\dfrac{17}{4}\\ =-\dfrac{5}{4}\)
\(B=\left(x_1-x_2\right)^2\\ =x_1^2+x_2^2-2x_1x_2\\ =\left(x_1+x_2\right)^2-4x_1x_2\\ =\left(\dfrac{1}{2}\right)^2-4.\left(-2\right)\\ =\dfrac{1}{4}+8\\ =\dfrac{33}{4}\)
\(D=\left(1+x_1\right)\left(2-x_1\right)+\left(1+x_2\right)\left(2-x_2\right)\\ =2+x_1-x_1^2+2+x_2-x_2^2\\ =4+\left(x_1+x_2\right)-\left(x_1^2+x_2^2\right)\\ =4+\dfrac{1}{2}-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =\dfrac{9}{2}-\left[\left(\dfrac{1}{2}\right)^2-2.\left(-2\right)\right]\\ =\dfrac{9}{2}-\dfrac{17}{4}\\ =\dfrac{1}{4}\)

\(a,2x^2+3x-9=0\\ \Leftrightarrow\left(2x^2+6x\right)-\left(3x+9\right)=0\\ \Leftrightarrow2x\left(x+3\right)-3\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(2x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{3}{2}\end{matrix}\right.\)
\(b,6x-12x^2=0\\ \Leftrightarrow6x\left(1-2x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
\(c,8x^2-1=0\\ \Leftrightarrow x^2=\dfrac{1}{8}\\ \Leftrightarrow x=\pm\dfrac{\sqrt{2}}{4}\)
\(d,x^4-7x^2-18=0\\ \Leftrightarrow\left(x^4-3x^3\right)+\left(3x^3-9x^2\right)+\left(2x^2-6x\right)+\left(6x-18\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x^3+3x^2+2x+6\right)=0\\ \Leftrightarrow\left(x-3\right)\left[x^2\left(x+3\right)+2\left(x+3\right)\right]=0\\ \Leftrightarrow\left(x-3\right)\left(x+3\right)\left(x^2+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\\x^2=-2\left(vô.lí\right)\end{matrix}\right.\)
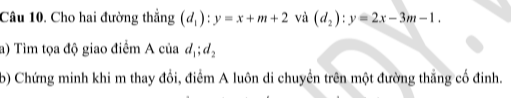 ai giup mik vs :<
ai giup mik vs :< 




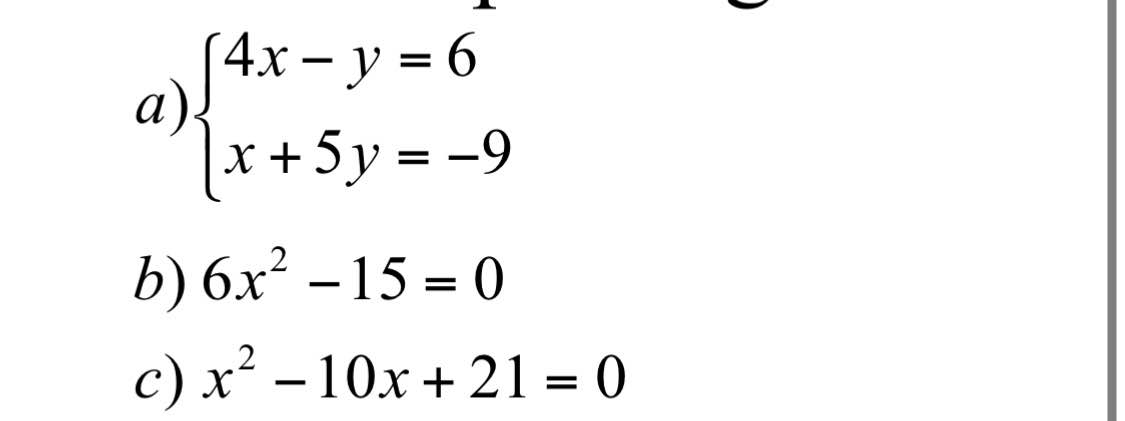 X
X