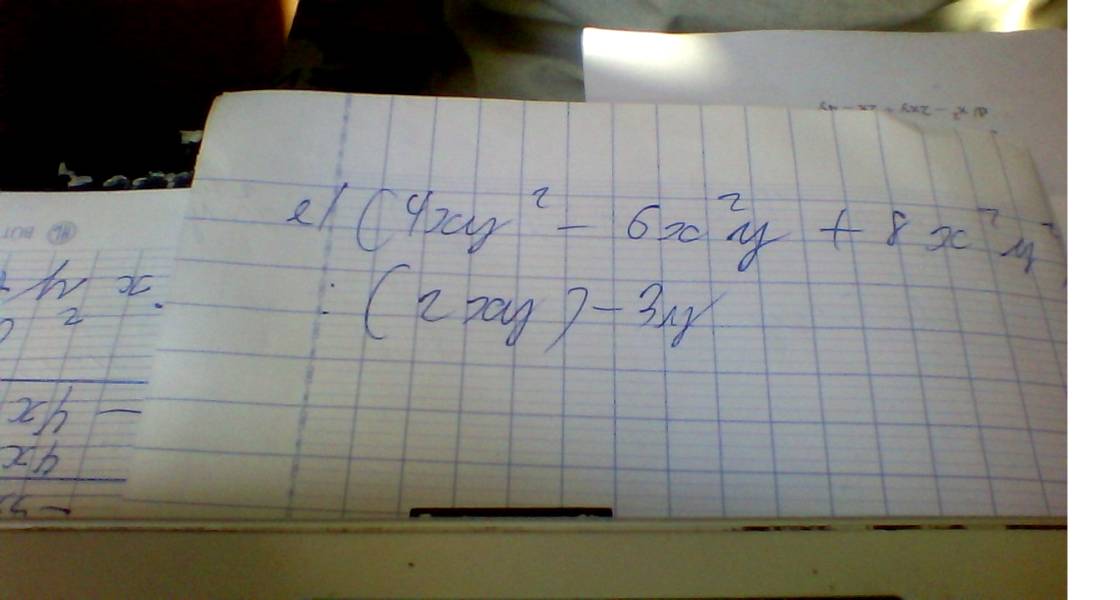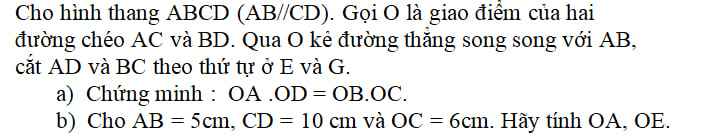Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xác định các số a,b,c sao cho 1/(x^2+z)(x-1)= (ax+b)/(x^2+1) +c/(x-1)
Giúp tớ nhanh với ạ, tớ cần gấp

Mình xin phép sửa đề 1 trust ạ :>
Xác định các số a,b,c sao cho \(\frac{1}{\left(x^2+1\right)\left(x-1\right)}=\frac{ax+b}{x^2+1}+\frac{c}{x-1}\)
Điều kiện x khác 1 :vv
\(pt\Leftrightarrow\frac{1}{\left(x^2+1\right)\left(x-1\right)}=\frac{\left(ax+b\right)\left(x-1\right)}{\left(x^2+1\right)\left(x-1\right)}+\frac{c\left(x^2+1\right)}{\left(x^2+1\right)\left(x-1\right)}\)
\(\Leftrightarrow1=ax^2-ax+bx-b+cx^2+c\)
\(\Leftrightarrow\left(a+c\right)x^2+\left(b-a\right)x+\left(c-b-1\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}a+c=0\\b-a=0\\c-b-1=0\end{cases}\Leftrightarrow}a=-\frac{1}{2};b=-\frac{1}{2};c=\frac{1}{2}\)
Vậy .....

\(AB=\sqrt{6^2+8^2}=10\left(cm\right)\)
BD là phân giác
=>CD/BC=DA/BA
=>CD/4=DA/5=6/9=2/3
=>CD=8/3cm; DA=10/3cm

- Xét △OBC có: \(BC\)//\(AD\) (gt).
=>\(\dfrac{OD}{OC}=\dfrac{OA}{OB}\) (định lí Ta-let).
=>\(OD=\dfrac{OA}{OB}.OC=\dfrac{2,5}{2}.3=3,75\) (cm).

Tớ ko giúp đc)): cọu tự tra google đuy,chứ có google để làm j ((:?

2A:
Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
góc ADH=góc CBK
=>ΔAHD=ΔCKB
=>AH=CK
AH vuông góc BD
CK vuông góc BD
=>AH//CK
Xét tứ giác AHCK có
AH//CK
AH=CK
=>AHCK là hình bình hành

1: Xét tứ giác BHCK có
CH//BK
BH//CK
Do đó: BHCK là hình bình hành
Suy ra: Hai đường chéo BC và HK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
2: Gọi giao điểm của IH và BC là O
Suy ra: IH\(\perp\)BC tại O và O là trung điểm của IH
Xét ΔHIK có
O là trung điểm của HI
M là trung điểm của HK
Do đó: OM là đường trung bình của ΔHIK
Suy ra: OM//IK
hay BC//IK
mà BC\(\perp\)IH
nên IH\(\perp\)IK
Xét ΔHOC vuông tại O và ΔIOC vuông tại O có
OC chung
HO=IO
Do đó: ΔHOC=ΔIOC
Suy ra: CH=CI
mà CH=BK
nên CI=BK
Xét tứ giác BCKI có IK//BC
nên BCKI là hình thang
mà CI=BK
nên BCKI là hình thang cân

a) Vì AB // CD ⇒ \(\widehat{ABD}=\widehat{ODC}\) ( 2 góc so le trong )
Hay \(\widehat{ABO}=\widehat{ODC}\)
Xét △ AOB và △ COD có:
\(\widehat{ABO}=\widehat{CDO}\) ( chứng minh trên )
\(\widehat{AOB}=\widehat{COD}\) ( đối đỉnh )
⇒ △ AOB ∼ △ COD ( g - g )
b) Vì △ AOB ∼ △ COD
⇒ \(\dfrac{OA}{OC}=\dfrac{AB}{CD}\Rightarrow\dfrac{OA}{6}=\dfrac{5}{10}\)
\(\Rightarrow OA=3cm\)
Vì OE // DC nên theo định lí Ta - lét ta có:
\(\dfrac{OE}{BC}=\dfrac{OA}{AC}\Rightarrow\dfrac{OE}{10}=\dfrac{3}{3+6}\)
\(\Rightarrow OE\approx3,3cm\)