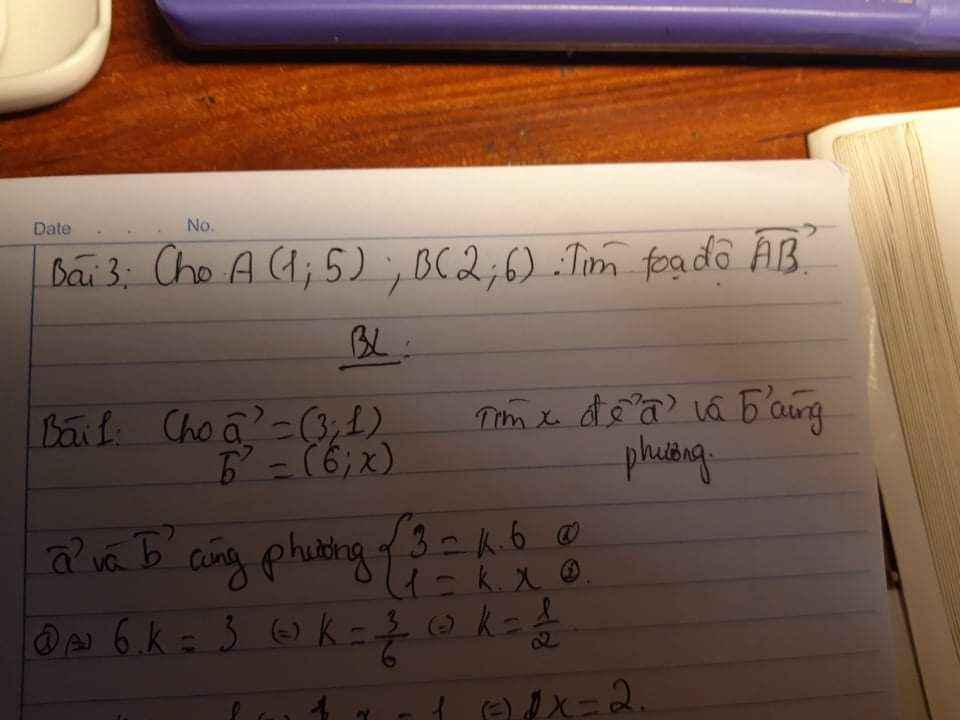K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 7 2021
5a.
Pt có 2 nghiệm pb lhi:
\(\Delta=9+4m>0\Leftrightarrow m>-\dfrac{9}{4}\)
b. Phương trình có 2 nghiệm khi:
\(\Delta=1+4\left(-2m+1\right)\ge0\Rightarrow m\le\dfrac{5}{8}\)
6.
a. Pt có 2 nghiệm khi:
\(\Delta'=1-\left(m+2\right)\ge0\Leftrightarrow m\le-1\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 7 2021
6b
Khi \(m\le-1\), theo hệ thức Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m+2\end{matrix}\right.\)
\(x^2_1+x^2_2=10\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4-2\left(m+2\right)=10\)
\(\Leftrightarrow m=-5\)
B.
\(x^2_1+x_2^2+4x_1x_2=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2+2x_1x_2=0\)
\(\Leftrightarrow4+2\left(m+2\right)=0\)
\(\Leftrightarrow m=-4\)
PK
5
TA
18 tháng 5 2021
`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)
HP
20 tháng 11 2021
a) (P) có đỉnh I(-1; -2)
\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{b}{2a}=-1\\-\dfrac{\Delta}{4a}=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=2.2\\b^2-4.2.c=8.2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\b^2-8c=16\end{matrix}\right.\Leftrightarrow4^2-8c=16\)
\(\Leftrightarrow c=0\)
=> y = 2x2 + 4x
b) (P) có trục đối xứng x = 1 và cắt trục tung tại M(0; 4)
\(M\in\left(P\right)\Rightarrow4=2.0^2+b.0+c\)
\(\Leftrightarrow c=4\)
Trục đối xứng: \(x=-\dfrac{b}{2a}=1\)
<=> -b = 2a
<=> -b = 2.2
<=> b = -4
=> y = 2x2 - 4x + 4
c) Đi qua 2 điểm A(1; 6), B(-1; 0)
\(A\in\left(P\right)\Rightarrow6=2.1^2+b.1+c\)
\(\Leftrightarrow b+c=4\) (1)
\(B\in\left(P\right)\Rightarrow0=2.\left(-1\right)^2+b\left(-1\right)+c\)
\(\Leftrightarrow-b+c=-2\) (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}b+c=4\\-b+c=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=3\\c=1\end{matrix}\right.\)
=> y = 2x2 + 3x + 1
21 tháng 12 2021
1: \(\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
22 tháng 10 2021
\(\overrightarrow{AB}=\left(2-1;6-5\right)=\left(1;1\right)\)
