Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 3:
Kẻ Oz//Ax thì Oz//By
Do đó \(\widehat{zOA}=\widehat{OAx}=32^0;\widehat{zOB}=180^0-\widehat{OBy}=58^0\)
\(\Rightarrow\widehat{AOB}=\widehat{zOA}+\widehat{zOB}=32^0+58^0=90^0\)
Vậy OA⊥OB

Bài 1. B = 1 + 2 + 3 + ... + 98 + 99
Số số hạng : ( 99 - 1 ) : 1 + 1 = 99 số
Tổng : ( 99 + 1 ) . 99 : 2 = 4950
=> B = 4950
Công thức
Tính số số hạng : ( số lớn - số bé ) : khoảng cách + 1
Tính tổng : ( số lớn + số bé ) . số số hạng : 2
=> Tương tự với C và D
Bài 1:
Dãy B có số số hạng là:(99-1):1 +1=99 số số hạng
=> B=\(\frac{\left(99+1\right)\cdot99}{2}=4950\)
Bài 2:
Dãy C có số số hạng là: (999-1):2+1=500 số số hạng
=> \(C=\frac{\left(999+1\right)\cdot500}{2}=250000\)
Bài 3: làm tương tự

6) \(\dfrac{8^6}{256}=\dfrac{\left(2^3\right)^6}{2^8}=\dfrac{2^{18}}{2^8}=2^{10}=1024\)
7) \(\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{4}\right)^{20}=\left(\dfrac{1}{2}\right)^{15}.\left[\left(\dfrac{1}{2}\right)^2\right]^{20}=\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{2}\right)^{40}=\left(\dfrac{1}{2}\right)^{55}=\dfrac{1}{2^{55}}\)
8) \(\left(\dfrac{1}{9}\right)^{25}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{50}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{20}=\dfrac{1}{3^{20}}\)
9)\(\left(\dfrac{1}{16}\right)^3\div\left(\dfrac{1}{8}\right)^2=\left(\dfrac{1}{2}\right)^{12}\div\left(\dfrac{1}{2}\right)^6=\left(\dfrac{1}{2}\right)^6=\dfrac{1}{64}\)
10) \(\dfrac{27^2.8^5}{6^2.32^3}=\dfrac{3^6.2^{15}}{3^2.2^2.2^{15}}=\dfrac{3^4}{2^2}=\dfrac{81}{4}\)

Câu 6.6 trang 19 Sách Bài Tập SBT Toán lớp 7 tập 1
Tính M=820+420425+645M=820+420425+645.
Giải
M=820+420425+645=(23)20+(22)20(22)25+(26)5M=820+420425+645=(23)20+(22)20(22)25+(26)5
=260+240250+230=240(220+1)230(220+1)=210=1024.=260+240250+230=240(220+1)230(220+1)=210=1024.
Câu 6.7 trang 19 Sách Bài Tập SBT Toán lớp 7 tập 1
Tìm x, biết:
a) (x4)2=x12x5(x≠0);(x4)2=x12x5(x≠0);
b) x10 = 25x8.
Giải
a) (x4)2=x12x5(x≠0)⇒x8=x7(x4)2=x12x5(x≠0)⇒x8=x7
⇒x8−x7=0⇒x7.(x−1)=0⇒x8−x7=0⇒x7.(x−1)=0
⇒x−1=0⇒x−1=0 (vì x7 ≠ 0)
Vậy x = 1.
b) x10=25x8⇒x10−25x8=0⇒x8.(x2−25)=0x10=25x8⇒x10−25x8=0⇒x8.(x2−25)=0
Suy ra x8 = 0 hoặc x2 - 25 = 0.
Do đó x = 0 hoặc x = 5 hoặc x = -5.
Vậy x∈{0;5;−5}x∈{0;5;−5}.
Câu 6.8 trang 19 Sách Bài Tập SBT Toán lớp 7 tập 1
Tìm x, biết:
a) (2x+3)2=9121(2x+3)2=9121;
b) (3x−1)3=−827(3x−1)3=−827
Giải
a) (2x+3)2=9121=(±311)2(2x+3)2=9121=(±311)2
Nếu 2x+3=311⇒x=−15112x+3=311⇒x=−1511
Nếu 2x+3=−311⇒x=−18112x+3=−311⇒x=−1811
b) (3x−1)3=−827=(−23)3(3x−1)3=−827=(−23)3
⇔3x−1=−23⇔x=19

Đặt A = 1 +3 +5 +...+(2n-1)
Số số hạng của A là : [(2n-1)-1]:2 +1 = n
Tổng A = [(2n-1)+1]xn:2=n2
=> n2=169
=>n2=132
=>n=13

b: \(=8+2\cdot3-7\cdot1.3+3\cdot\dfrac{5}{4}=8.65\)

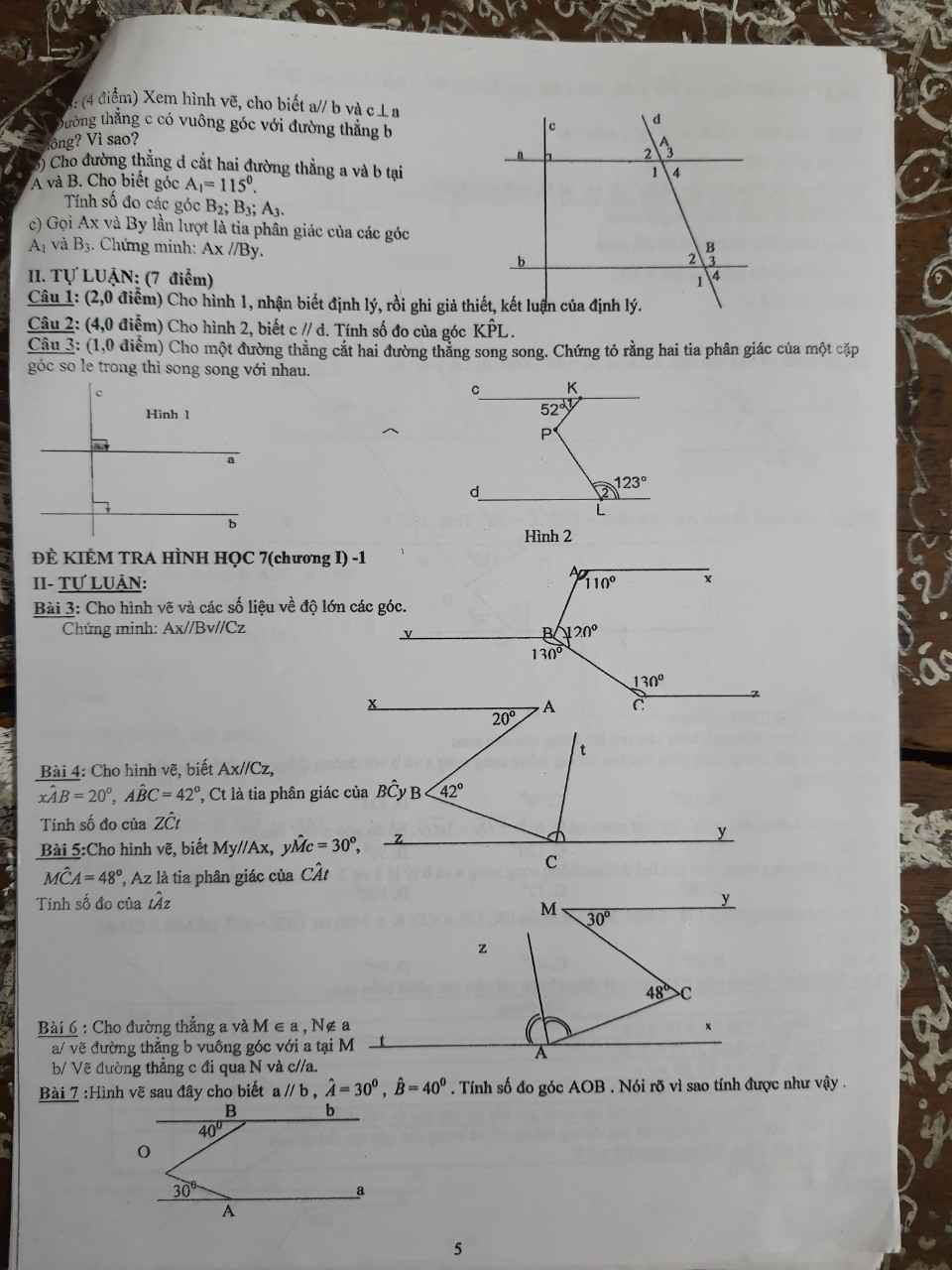



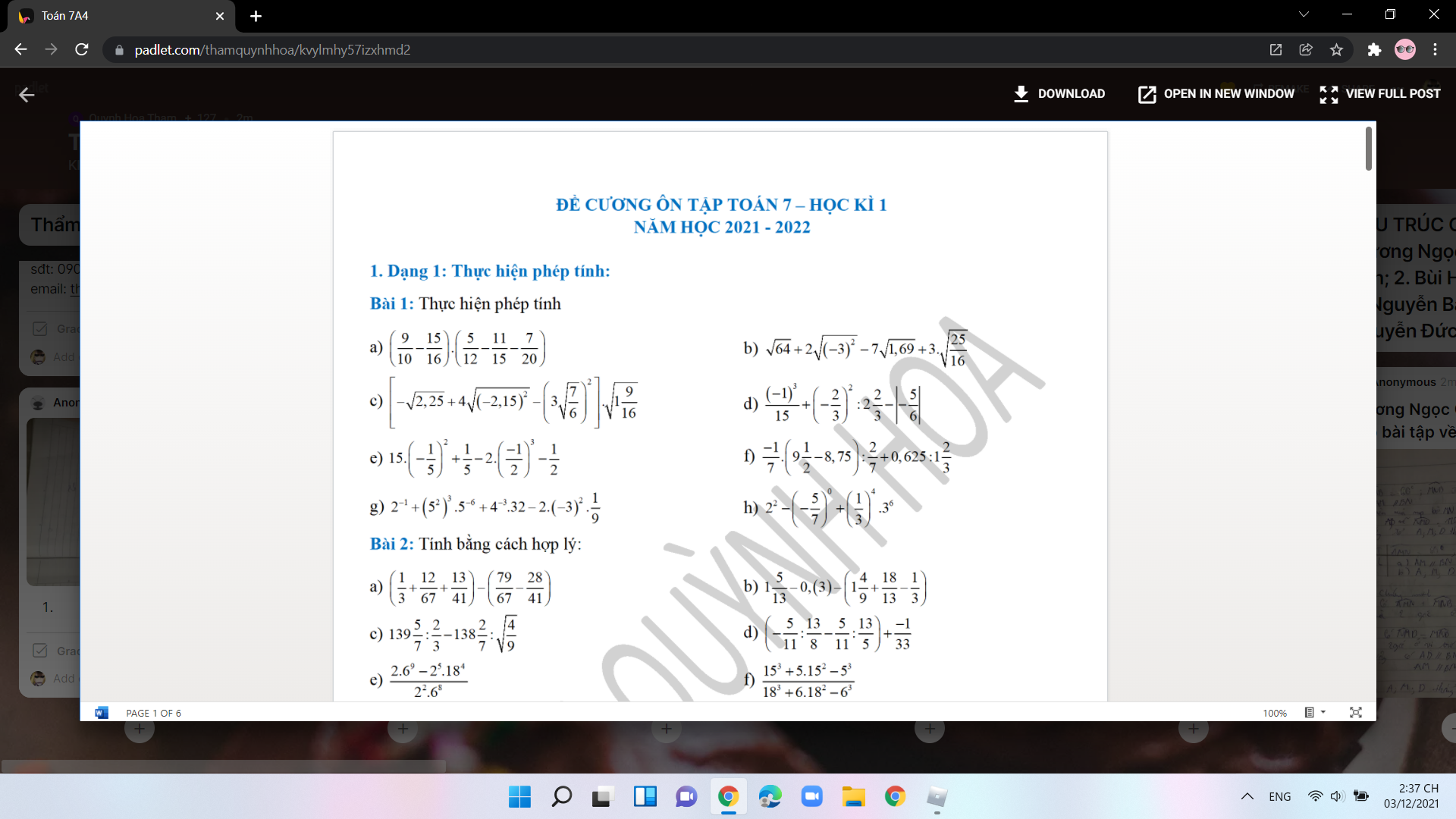 làm giúp mình bài 1 với, mình cần gấp ( nếu rảnh làm hộ mình bài 2 cũng dc )
làm giúp mình bài 1 với, mình cần gấp ( nếu rảnh làm hộ mình bài 2 cũng dc )
mik chỉ bt nhiêu đó thui, bn thông cảm