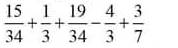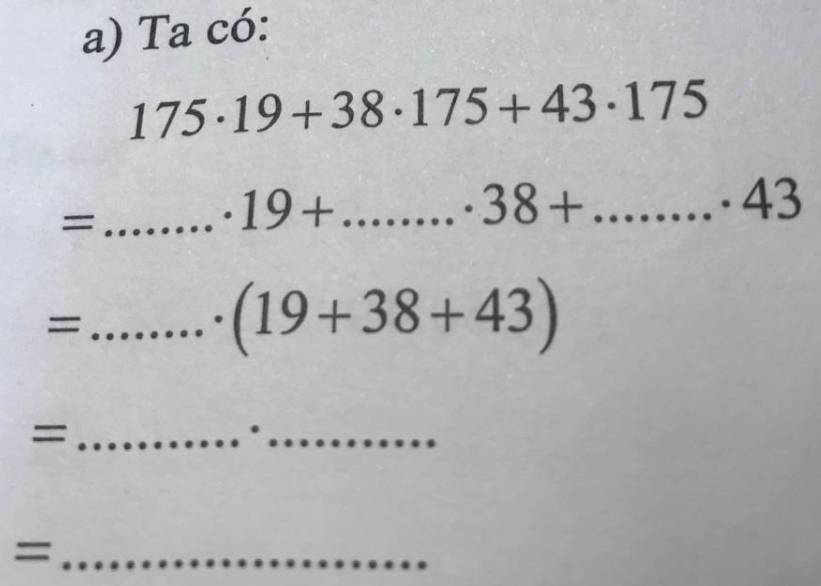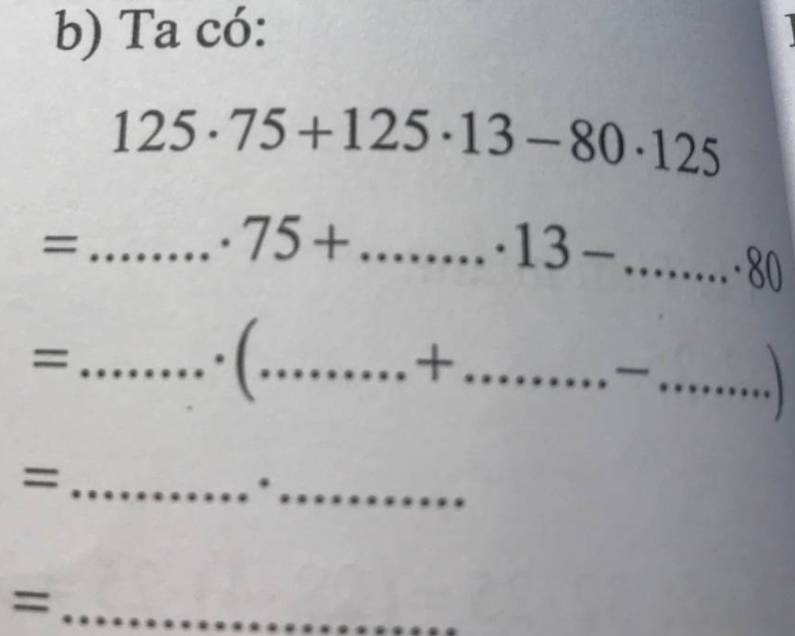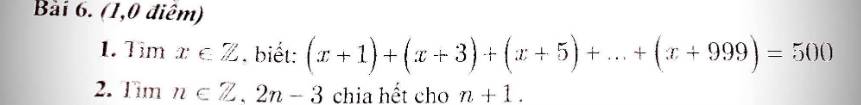TT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TA
0
NM
Nguyễn Minh Quang
Giáo viên
17 tháng 10 2021
bài 4.
a. hai tam giác đều là OAB,OCD
hai hình thoi là ABOF và BCOA
hai hình chữ nhật là :ABDE và ACDF
b.\(S_{ABDE}+S_{AOEF}=AB\times AE+\frac{1}{2}AB\times AE=21060cm^2\)
bài 5. ta có
\(n^2+n=n\left(n+1\right)\text{ luôn là số chẵn với mọi n do hai số tự nhiên liên tiếp luôn có 1 số chẵn}\)
nên \(n^2+n+1\text{ luôn là số lẻ}\)
1 tháng 9 2021
Bài 1 :
a) \(1-\left(5\frac{3}{8}+x-6\frac{5}{24}\right):12\frac{2}{5}=0\)
\(\Rightarrow\left(\frac{43}{8}+x-\frac{149}{24}\right):\frac{62}{5}=1\)
\(\Rightarrow\left(\frac{129}{24}-\frac{149}{24}\right)+x=\frac{62}{5}\)
\(\Rightarrow\frac{-5}{6}+x=\frac{62}{5}\)
\(\Rightarrow x=\frac{62}{5}-\frac{-5}{6}=\frac{397}{30}\)
1 tháng 9 2021
Xin lỗi , mình không biết làm phần c bài 1
Bài 2 :
Ta có : \(A=\left(-\frac{1}{7}\right)+\left(-\frac{1}{7}\right)^2+...+\left(-\frac{1}{7}\right)^{10}\)
\(\Rightarrow7A=-1+\left(-\frac{1}{7}\right)+\left(-\frac{1}{7}\right)^2+...+\left(-\frac{1}{7}\right)^9\)
\(\Rightarrow7A-A=\left[-1+\left(-\frac{1}{7}\right)+\left(-\frac{1}{7}\right)^2+...+\left(-\frac{1}{7}\right)^9\right]-\left[\left(-\frac{1}{7}\right)+\left(-\frac{1}{7}\right)^2+...+\left(-\frac{1}{7}\right)^{10}\right]\)
\(\Rightarrow6A=-1-\left(\frac{-1}{7}\right)^{10}\Rightarrow A=\frac{-1-\left(\frac{-1}{7}\right)^{10}}{6}\)
GD
Mình cảm ơn ạ
2
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
24 tháng 1 2024
\(\dfrac{15}{34}+\dfrac{1}{3}+\dfrac{19}{34}-\dfrac{4}{3}+\dfrac{3}{7}=\left(\dfrac{15}{34}+\dfrac{19}{34}\right)+\left(\dfrac{1}{3}-\dfrac{4}{3}\right)+\dfrac{3}{7}=1-1+\dfrac{3}{7}=\dfrac{3}{7}\)
D
datcoder
CTVVIP
14 tháng 10 2023
a)
\(175\cdot19+38\cdot175+43\cdot175\\ =175\cdot19+175\cdot38+175\cdot43\\ =175\cdot\left(19+38+43\right)\\ =175\cdot100\\ =17500\)
b)
\(125\cdot75+125\cdot13-80\cdot125\\ =125\cdot75+125\cdot13-125\cdot80\\ =125\cdot\left(75+13-80\right)\\ =125\cdot10\\ =125\cdot8\\ =1000\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 10 2023
a, 175. 19 + 38. 175 + 43. 175
= 175. 19 + 175. 38 + 175. 43
= 175.(19 + 38 + 43)
= 175. 100
= 17500
GH
0
D
datcoder
CTVVIP
5 tháng 12 2023
2/
Xét phân số \(\dfrac{2n-3}{n+1}=\dfrac{2n+2-5}{n+1}=\dfrac{2n+2}{n+1}-\dfrac{5}{n+1}=\dfrac{2\left(n+1\right)}{n+1}-\dfrac{5}{n+1}=2-\dfrac{5}{n+1}\)
\(n\in Z\Rightarrow2n-3\inƯ\left(5\right)=\left\{-1;-5;1;5\right\}\)
Ta có bảng:
| 2n - 3 | -1 | -5 | 1 | 5 |
| n | 1 | -1 | 2 | 4 |
Vậy \(n\in\left\{-1;1;2;4\right\}\)
D
datcoder
CTVVIP
5 tháng 12 2023
1/
(x + 1) + (x + 3) + (x + 5) + ... + (x + 999) = 500
<=> (x + x + x + ... + x) + (1 + 3 + 5 + ... + 999) = 500
Xét tổng A = 1 + 3 + 5 + ... + 999
Số số hạng của A là: (999 - 1) : 2 + 1 = 500
Tổng A là: (999 + 1) x 500 : 2 = 250 000
Do A có 500 số hạng nên có 500 ẩn x.
Vậy ta có: 500x + 250 000 = 500
=> 500x = -249 500
=> x = 499
Vậy x = 499
