
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x+3}{x-y}.\dfrac{x^2-y^2}{x^2-9}=\dfrac{x+3}{x-y}.\dfrac{\left(x-y\right)\left(x+y\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{x+y}{x-3}\)


5:
a: \(\Leftrightarrow A-B+2xy^2-x^2y=3x^2y\)
=>\(A-B=3x^2y+x^2y-2xy^2=4x^2y-2xy^2\)
b: \(\Leftrightarrow A-B-\dfrac{3}{8}xy^2=\dfrac{3}{4}xy^2-\dfrac{1}{2}xy^2=\dfrac{1}{4}xy^2\)
=>\(A-B=\dfrac{1}{4}xy^2+\dfrac{3}{8}xy^2=\dfrac{5}{8}xy^2\)
c: \(\Leftrightarrow-2x^2y^3-\left(A-B\right)=8x^3y^2\)
=>\(A-B=-2x^2y^3-8x^3y^2\)

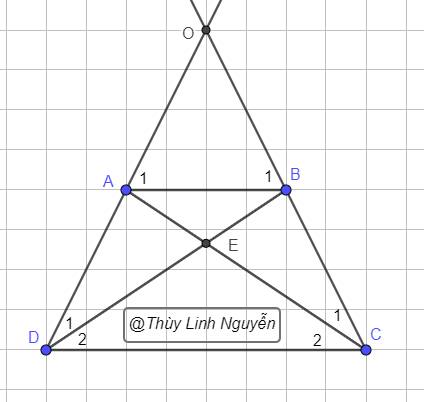
`a,`
Có `AB////CD(g t)`
`=>{(hat(A_1)=hat(ADC)(Sol etrong)),(hat(B_1)=hat(BCD)(Sol etrong)):}`
Mà `hat(ADC)=hat(BCD)` (Tứ giác `ABCD` là hình thang cân)
Nên `hat(A_1)=hat(B_1)`
`=>Delta OAB` cân tại `O(dpcm)`
`b,`
Tứ giác `ABCD` là hình thang cân `(g t)`
`=>hat(BAD)=hat(ABC);AD=BC`
Xét `Delta ABD` và `Delta BAC` có :
`{:(AB-chung),(hat(BAD)=hat(BAC)(cmt)),(AD=BC(cmt)):}}`
`=>Delta ABD=Delta BAC(c.g.c)(dpcm)`
`c,`
Có `Delta ABD=Delta BAC(cmt)`
`=>hat(D_1)=hat(C_1)` (2 góc tương ứng)
mà `hat(ADC)=hat(BCD)(cmt)`
Nên `hat(ADC)-hat(D_1)=hat(BCD)-hat(C_1)`
hay `hat(D_2)=hat(C_2)`
`=>Delta EDC` cân tại `E`
`=>ED=EC(dpcm)`
Hình:

1: =>x^2-5x+6-x^2-5x-6=x^2+1-x^2+9
=>-10x=10
=>x=-1(nhận)
2: \(\Leftrightarrow3x^2-15x-x^2+2x-2x^2=0\)
=>-13x=0
=>x=0
3: \(\Leftrightarrow13\left(x+3\right)+x^2-9=12x+42\)
=>x^2-9+13x+39-12x-42=0
=>x^2+x-12=0
=>(x+4)(x-3)=0
=>x=3(loại) hoặc x=-4(nhận)
4: \(\Leftrightarrow-2+x^2-5x+4=x^2+x-6\)
=>-5x-2=x-6
=>-6x=-4
=>x=2/3


\(\left(x-1\right)\left(x+1\right)\left(x+3\right)\)
\(=\left(x^2-1\right)\left(x+3\right)\)
\(=x^3+3x^2-x-3\)

1:
a: =x^2+3x+4x+12
=x(x+3)+4(x+3)
=(x+3)(x+4)
b: =4x^2-4x-5x+5
=4x(x-1)-5(x-1)
=(x-1)(4x-5)
c: =2x^2-3x-4x+6
=x(2x-3)-2(2x-3)
=(2x-3)(x-2)
3:
a: =2x^2-6xy+xy-3y^2
=2x(x-3y)+y(x-3y)
=(x-3y)(2x+y)
b: =x^2+3xy-xy-3y^2
=x(x+3y)-y(x+3y)
=(x+3y)*(x-y)
c: =6x^2+4xy-3xy-2y^2
=2x(3x+2y)-y(3x+2y)
=(3x+2y)(2x-y)

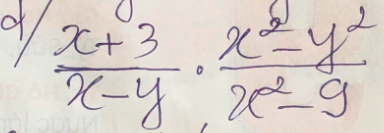

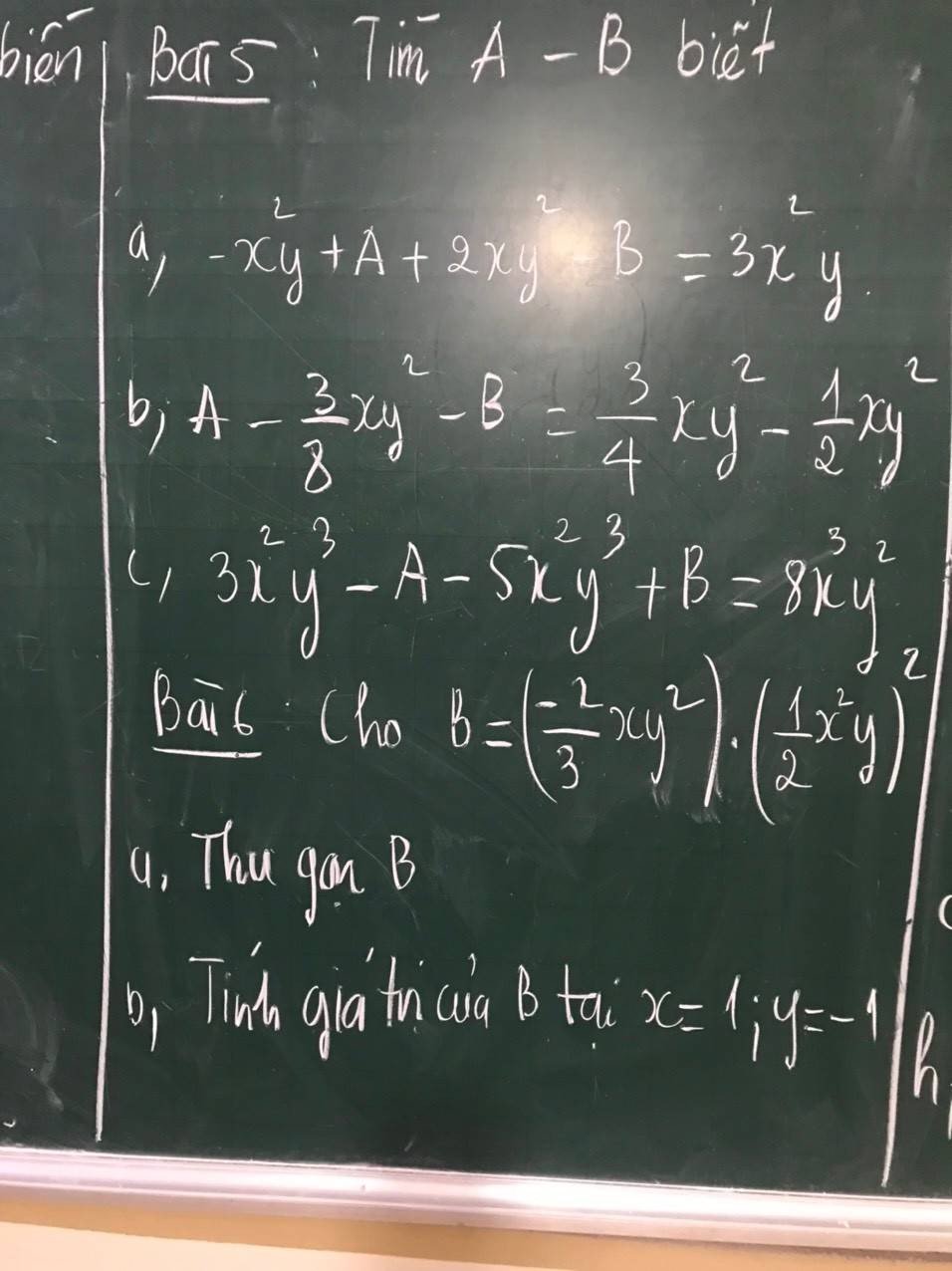

 ai giúp mik bài này đc ko ạ, mik cảm ơn!
ai giúp mik bài này đc ko ạ, mik cảm ơn!
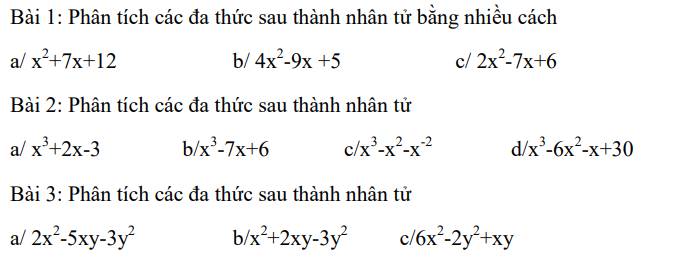
Bài 3:
a: \(=\dfrac{x-2+x}{2x-4}=\dfrac{2x-2}{2x-4}=\dfrac{x-1}{x-2}\)
b: \(=\dfrac{6}{5\left(x-4\right)}-\dfrac{x-5}{\left(x-4\right)^2}\)
\(=\dfrac{6x-24-5x+25}{5\left(x-4\right)^2}=\dfrac{x+1}{5\left(x-4\right)^2}\)
c: \(=\dfrac{3x+2-12x+8+3x-6}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{-6x+4}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{-2}{3x+2}\)